|
Thomas Bugge:
De første grunde til Regning, Geometrie,
Plan-Trigonometrie og Landmaaling.
Kiøbenhavn 1795.
Download dette dokument i Word-format.
Download dette dokument i
pdf-format.
Tredie Kapitel
Skievvinklede Trianglers Opløsning.
__________________________________________________________
§.21.
Tab.17.
Fig.259.
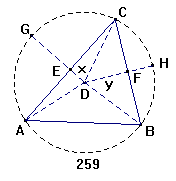
I enhver retlinet flad Triangel ABC forholde sig Siderne AC og BC som Sinus
af de modstaaende Vinkler, det er, som Sinus af B til Sinus af A, eller AC : BC
= sin.B : sin.A.
Den givne Triangel ABC indskrives i en Cirkel, hvis Center er D. Derfra drager
man paa Chorderne 1) AC og BC Perpendikularerne 2)
DE og DF. Disse skiære saavel Chorderne som Buerne i lige Dele (§.108 Geom 3));
saa at 2 CE = AC, og 2 BF = CB; ligeledes x = ½ ADC, og y = ½ BDC; nu er den
hele Vinkel ved Peripherien saa stor som den halve Center-Vinkel (§.121 Geom.4)),
eller ½ ADC = B og ½ BDC = A; hvoraf følger, at x = B og y = A. Af de
Trigonometriske Liniers Natur er det klart, at CE er Sinus til x, og BF til y (§.2);
eller BF = sin.y = sin.A, og CE = sin.x = sin.B; altsaa sin.B : sin.A = CE : BF
= 2 CE : 2 BF = AC : CB.
§.22.
Fig.260.
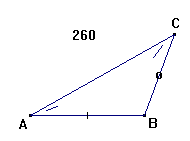
Naar i en skievvinklet Triangel gives en Side AB, og Vinkelen C lige over for
Siden AB, og desuden en af Vinklerne A ved samme Side, at finde den lige over
for staaende Side BC.
Man opsætter følgende Forhold: som sinus af Vinkelen C til den modstaaende
Side AB, saaledes Sinus af den anden givne Vinkel A til sin modstaaende Side BC,
eller
sin.C : AB = sin.A : BC (§.21).
F.Ex. AB = 2354 Alen 5) , A = 320 20´, C = 500
34´ 6) ,
Sin.500 34´ : 2354 = sin.32. 20 : BC
Log.2354 = 3.371806 7)
Log.sin.320 20´= 9.728227
13.100033
Log.sin. 500 34´= 9.887822
Log.BC = 3.212211
BC = 1630,1 Alen.
§.23.
Fig.261.
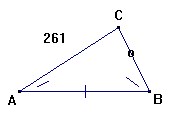
Dersom der gives Grundlinien AB, og begge Vinklerne ved Grundlinien A og B,
da at finde tvende Sider BC og AC.
1. Ved at lægge begge Vinklerne ved Grundlinien A og B sammen, og ved at drage
dem fra tvende rette Vinkler alle 1800, finder man Vinkelen C, som
staaer lige over for Grundlinien AB (§.67 Geom.8) )
2. Da har man samme givne Ting, som i §.22, og altsaa sin.C : AB = sin.A : BC,
og sin.C : AB = sin.B : AC.
F.Ex. AB = 10070 Alen, A = 570 54´ 45´´ og B = 530 14´
3´´; saa søger man først Vinkelen C.
A = 570 54´ 45´´
B = 53 14 : 3
A + B = 111. 8. 48
A + B + C = 179. 59.60 = 1800
C = 68. 51. 12
sin.C : AB = sin.A : BC
sin. 680 51´ 12´´ : 10070 = sin.570 54´ 45´´ : BC
log.10070 = 4.0030295
log.sin. 57.54.45 = 9.9280053
13.9310348
log.sin.86.51.12 = 9.9697233
log.BC = 3.9613115
BC = 9147,7 Alen
sin.680 51´ 12´´ : 10070 = sin. 530 14´ 3´´ : AC
log.10070 = 4.0030295
log.sin. 530 14´ 3´´ = 9.9036804
13.9067099
log.sin.68.51.12 = 9.9697233
log.AC = 3.9369866
AC = 8649,4
§.24.
Fig.262.
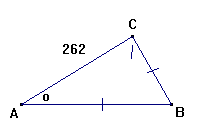
Naar i en Triangel ABC gives tvende Sider AB og BC, og en Vinkel C lige over for
den ene givne Side AB, da at finde den Vinkel A, som staaer lige over for den
anden givne Side BC.
Man finder Vinkelen A ved følgende Forhold:
AB : sin.C = CB : sin.A.
F.Ex. AB = 25394 Alen; C = 560 30´; CB = 4876 Alen.
5394 : sin.560 30´ = 4876 : sin.A
log.4876 = 3.688064
log.sin.560 30´= 9.921107
13.609171
log.5394 = 3.731911
log.sin.A = 9.877260
A = 480 55´ 16´´
Anmærkning. Naar man saaledes har fundet Vinkelen A,
og man tager Summen eller A + C fra 1800, har man den tredie Vinkel B
(§.67 Geom.8) ); og da kan man deraf søge den tredie Side
AC, nemlig sin.C : AB = sin.B : AC (§.22.). Paa den Maade har man fundet alle
Vinkler og Sider i Trianglen ABC; i øvrigt kan man lægge Mærke til, at naar
man vil søge en Vinkel, begynder Forholden med en Side, og naar man vil søge
en Side, begynder Forholden med en Vinkel.
§.25.
Tab.17.
Fig.263.
Naar der ere tvende ulige Størrelser M = 8 og m = 2, og man ved deres Summe S =
M + m = 10, og deres Difference D = M - m = 6, saa er den større M lige stor
med den halve Summe tilligemed den halve Difference, eller M = ½ S + ½ D =
10/2 + 6/2 = 5 + 3 = 8; og den mindre Størrelse er den halve Summe mindre end
den halve Difference, eller m = ½ S - ½ D = 10/2 - 6/2 = 5 - 3 = 2.
1. S = M + m og D = M - m; disse lægges sammen, saa er S + D = 2 M + m - m = 2
M, fordi + m, som er lagt til, nødvendigen tilintetgøres eller hæves ved - m,
som er subtraheret; man dividerer med 2, saa er M = ½ S + ½ D.
2. M + m = S; isteden for M sættes dens Værdie = ½ S + ½ D; altsaa ½ S + ½
D + m = S; man fradrager ½ S paa begge Sider, saa er ½ D + m = S - ½ S = ½
S; man fradrager ½ D paa begge Sider, saa er endeligen m = ½ S - ½ D.
§.26.
Fig.263.
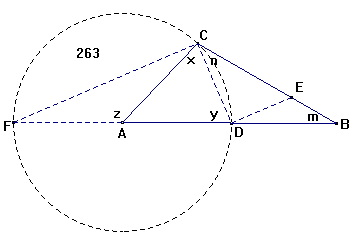
Naar udi en Triangel ABC gives tvende Sider AB og AC, og den af dem indbefattede
Vinkel BAC eller A, da at finde de øvrige Vinkler ved C og B.
1. Man lægger begge de givne Sider sammen, og finder deres Summa AB + AC.
2. Man tager dem fra hinanden, og finder deres Difference AB - AC.
3. Man tager den givne Vinkel A fra 1800, saa har man Summen af de
tvende ubekiendte Vinkler C + B (§.66 Geom. 9))
4. Man giør følgende Forhold som Summen af Siderne AB + AC til deres Forskiel
AB - AC, saaledes Tangens af de ubekiendte Vinklers halve Summer til Tangens af
disse Vinklers halve Difference, eller AB + AC : AB - AC = tang.½(C + B) :
tang.½(C - B).
5. Naar man saaledes har fundet de ubekiendte Vinklers halve Difference ½ C -
½ B; lægger man til deres halve Summe ½ C + ½ B den halve Difference ½ C -
½ B, saa har man den større af de søgte Vinkler= C; og naar man fra den halve
Summe ½ C + ½ B tager den halve Difference ½ C- ½ B, har man den mindre af
de ubekiendte Vinkler = B (§.25.).
Beviis. Det som behøver Beviis i denne Opløsning, er den under Num. 4
anførte Forhold, hvilken saaledes bevises. Fra A, som Center, og med den mindre
Side AC, som Radius, beskriver man en Cirkel, saa er BF Summen af de givne Sider
AB og AC, thi BF = AB + AF = AB + AC (§.14 Geom.10) ), og DB
er de givne Siders Difference; thi DB = AB - AD = AB - AC. Man drager FC og CD,
samt DE parallel med FC (§.65 Geom.11)). Da AC = AD, saa er x
= y (§.39 Geom.12)); men y = m + n (§.66 Geom. 9))
i  ABC, men i ABC, men i  ADC
er z = x + y (§66. Geom) = 2y, og ½ z = y,
altsaa x = m + n. Først fradrages m paa begge Sider, og x - m = n, dernæst
lægges n til paa begge Sider, saa er x + n - m = 2 n; men x + n = ACB = C og m
= ABC = B, altsaa C - B = 2 n; og ½ C - ½ B = n, eller n er de ubekiendte
Vinklers halve Difference. Fremdeles er z = ACB + ABC (§.66 Geom. 9)
) = 2 y, og ½ z = y; altsaa ½ z = y = ½ ACB + ½ ABC = ½ C + ½ B, eller y
er de ubekiendte Vinklers halve Summe. Videre da Vinkelen FCD er en Vinkel i en
halv Cirkel, saa er FCD = 900 (§.122 Geom.13) ),
eller FC perpendikular til CD; og naar CD antages som Radius, er FC = tang.y =
tang.(½ C + ½ B) (§.4). Nu er FC parallel med DE (Konstr.); og
Vexelvinklerne 14) lige store FCD = CDE (§.60 Geom.15)
); og naar CD er Radius, er DE = tang.n = tang.(½ C - ½ B). Fremdeles da DE er
parallel med FC saa er ADC
er z = x + y (§66. Geom) = 2y, og ½ z = y,
altsaa x = m + n. Først fradrages m paa begge Sider, og x - m = n, dernæst
lægges n til paa begge Sider, saa er x + n - m = 2 n; men x + n = ACB = C og m
= ABC = B, altsaa C - B = 2 n; og ½ C - ½ B = n, eller n er de ubekiendte
Vinklers halve Difference. Fremdeles er z = ACB + ABC (§.66 Geom. 9)
) = 2 y, og ½ z = y; altsaa ½ z = y = ½ ACB + ½ ABC = ½ C + ½ B, eller y
er de ubekiendte Vinklers halve Summe. Videre da Vinkelen FCD er en Vinkel i en
halv Cirkel, saa er FCD = 900 (§.122 Geom.13) ),
eller FC perpendikular til CD; og naar CD antages som Radius, er FC = tang.y =
tang.(½ C + ½ B) (§.4). Nu er FC parallel med DE (Konstr.); og
Vexelvinklerne 14) lige store FCD = CDE (§.60 Geom.15)
); og naar CD er Radius, er DE = tang.n = tang.(½ C - ½ B). Fremdeles da DE er
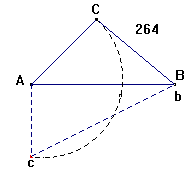
parallel med FC saa er  BFC ~ BFC ~ 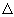 BDE,
og BF : BD = FC : DE (§.148 Geom.15) ); men BF = AB + AC og
BD = AB - AC efter hvad som forhen er beviist; derfor AB + AC : AB - AC =
tang.(½C + ½B) : tang.(½C - ½B). BDE,
og BF : BD = FC : DE (§.148 Geom.15) ); men BF = AB + AC og
BD = AB - AC efter hvad som forhen er beviist; derfor AB + AC : AB - AC =
tang.(½C + ½B) : tang.(½C - ½B).
Exempel. AB = 693 Fod. AC = 539 Fod. A = 410 37´.
AB = 693
A + B + C = 1790.60´
AC = 539
A = 41. 37
AB + AC = 1232
Fod C + B = 138.23.
AB - AC = 154 Fod
½ C + ½ B = 690.11´.30´´
1232 : 154 = tang.690.11´.30´´ : tang. ½ C - ½ B.
log.154 = 2.1875207
log.tang.690.11´.30´´ = 10.4201812
12.6077019
log.1232 = 3.09006107
log.tang.(½ C - ½ B) = 9.5170912
½ C - ½ B = 130 12´.26´´
½ C + ½ B = 69. 11. 30
C = 87. 23. 56
B = 50. 59. 4
Saaledes har man fundet de tvende Vinkler C og B. Vil man videre end finde den
tredie Side BC, da skeer det ved følgende Forhold:
Sin.B : AC = sin.A : BC (§.22)
sin.500.59´.4´´ : 539 = sin.410.37´: BC
log.539 = 2.7315888
log.sin.410.37 = 9.8222621
12.5538509
log.sin.500.59´.4´´ = 9.8904071
log.BC = 2.6634438
BC = 460,73 Fod.
§.27.
Tab.17.
Fig.264.
Naar der udi en Triangel ABC gives tvende Sider AB og AC, og den indbefattede
Vinkel BAC, kan man endnu paa en anden og følgende Maade finde de tvende
øvrige Vinkler B og C.
1. Som den mindste Side AC er til den største Side AB, saaledes Sinus Totus til
Tangens af en Vinkel c.
2. Fra denne Vinkel drager man 450, og Forskiellen x = c - 450.
3. Fremdeles: som Sinus Totus til Tangens af c - 450 eller Tangens x,
saaledes Tangens af de søgte Vinklers halve Summe til Tangens af deres halve
Difference.
4. Af den halve Summe og den fundne halve Difference findes den store Vinkel C
og den mindre B.
F.Ex., AB = 693 Fod, AC = 539 Fod, A = 410.37´, saa er AB + AC =
1232 Fod; AB - AC = 154 Fod; ½ C + ½ B = 690 11´.30´´ (§.26
Exemp.)
AC : AB = R : tang.c
539 : 693 = sin.tot. : tang.c
log.sin.tot. + log.693 = 12.8407332
log.539 = 2.7315888
log.tang.c = 0.1091444
c = 520. 7´.30
450 = 450
x = c - 450 = 70.7´.30
R : tang.(c - 450) = tang.(½ C + ½ B) : tang.(½ C - ½ B)
Sin.tot. : t.70 7´.30´´ = t.690 11´.30 : t.(½ C - ½
B)
Log.tang.690.11´30´´ = 10.4201812
Log.tang. 7 . 7 . 30 = 9.0969090
Log.tang. (½ C - ½ B) = 9.5170902
½ C - ½ B = 180 12´. 26´´
Ganske saaledes , som forhen er fundet.
Beviis………
§.28.
Fig.265.
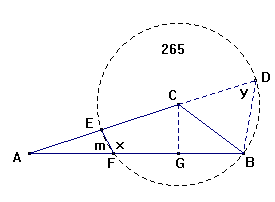
Naar der i en Triangel ABC gives alle trende Sider AB, BC og AC, da at finde
Vinklerne.
1. Fra toppen af den første Vinkel C nedlader man paa den modstaaende største
Side AB en Perpendikular CG, og fra C, som Center, mod den mindste Side BC, som
Radius, beskrives en Cirkel.
2. Man opsætter følgende Forhold: som den største Side AB til Summen af de
andre Sider AC + CB; saaledes disse Siders Forskiel AC - CB til Stykket uden for
Cirkelen AF.
3. Dette Stykke AF tages fra AB, saa har man BF; og ½ BF = FG = BG (§ 108
Geom.17)); og AG = AF + FG = AF + ½ BF.
4. I den retvinklede Triangel BCG findes Vinkelen B ved følgende Forhold: CB :
BG = R : cos.B (§ 14).
5. Iden retvinklede Triangel AGC søges Vinkelen A ved dette Forhold: AC : AG =
R : cos.A (§ 14).
6. Endeligen findes BCA = 180 - (A + B) (§.67 Geom.18))
Beviis. Det som i denne Opløsning behøver Beviis, er at AB : AC + CB = AC
- CB : AF. Nu er AD = AC + CD = AC + CB; og AE = AC - CE = AC - CB. Fremdeles x
= ½ EDB og y = ½ BFE ( § 122 Geom.19)) ; altsaa x + y = ½
EDB + ½ BFE = 1800 (§ 20 Geom.20)) = m + x (§ 31
Geom.21)), og naar man fradrager x, bliver y = m. End videre
er Vinkelen A tilfælles for 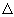 ABD
og ABD
og 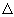 AEF; altsaa AEF; altsaa 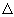 ABD
~ ABD
~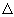 AEF (§ 149 Geom.22))
og AB : AD = AE : AF, eller AB : AC + CB = AC - CB : AF. AEF (§ 149 Geom.22))
og AB : AD = AE : AF, eller AB : AC + CB = AC - CB : AF.
Exempel. AC = 354 Fod; BC = 346 Fod og AB = 625 Fod.
AC = 354 Fod
AC = 354 Fod
BC = 346
BC = 346
AC + BC = 700 Fod AC - BC = 8 Fod
AB : AC + BC = AC - BC : AF
625 : 700 = 8 : AF
log.8 = 0.9030900
log.700 = 2.8450980
3.7481880
log.625 = 2.7958800
log.AF = 0.9523080
AF = 8,96 Fod
AB = 625 Fod
AF = 8,96
BF = 616,04
BG = ½ BF = 308,02
AG = AF + ½ BF = 316,98
CB : BG = R : cos.B
346 : 308,02 = sin.tot : cos.B
log.sin.tot. + log.308,02 = 12.4885789
log.346 = 2.5390761
log.cos.B = 9.9495028
B = 270. 5´.52
AC : AG = R : cos.A
354 : 316,98 = sin.tot. : cos.A
log.sin.tot. + log.316,98 = 12.5000319
log.354 = 2.5490033
log.cos.A = 9.9520286
A = 260. 16´.14
B = 27. 5. 52
A = 26. 26. 14
A + B = 53. 32. 06
C + A + B = 179. 59. 60
C = 126.27.54
_______________________________________________________________________
Noter:
1) Chorde: Et linjestykke der forbinder to punkter på en
cirkelperiferi.
2) Perpendikular: En linje der står vinkleret på en anden linje.
3) § 108 Geom:
Naar Diameteren DE er Perpendikular til Chorden AB, saa deler den Chorden AB i
tvende lige Dele, AF = FB……
4) § 121 Geom:
Vinkelen ved Centeret ACB er dobbelt saa stor som Vinklen ved Peripherien ADB,
naar de begge staae paa samme Bue AB……
5) Målestoksforhold:
1 Fod = 10 decimaltommer = 100 decimallinier = ½ Alen.1 Alen = 62.8 cm.
6) Vinkelmål:
En hel cirkel deles i 3600.
Hver grad deles i 60 bueminutter ( skrives 60´) og hvert bueminut deles i 60
buesekunder (skrives 60´´).
F.eks. betyder 200 13´45 ´´ : 20 grader, 13 minutter og 45
sekunder
Eksempel på omregning:
200 13´ 45´´ = 20 + 13 / 60 + 45 / 602 = 20.22916670.
Tilbageskrivningen af 20.22916670 ser sådan ud:
20.2291667 - 20 = 0.2291667 (træk heltalsværdien fra)
0.2291667H 60 = 13.75000
(multiplicer
med 60)
13.75000 - 13 = 0.7500
(træk heltalsværdien fra)
0.7500 H 60 = 45.000
(multiplicer med
60)
7) Se Beregning med logaritmer
8) § 67 Geom:
… Naar der i en Triangel ABC gives tvende Vinkler A og B, saa findes den tredie Vinkel C ved at drage de tvende givne Vinklers Summa fra tvende rette
Vinkler…..
9) § 66 Geom
Naar i enhver Triangel ABC den ene Side AB forlænges til D, er den udvendige
Vinkel DBC saa stor som de tvende indvendige og modstaaende Vinkler A + C, og
alle Vinkler tilsammentagne er saa store som tvende rette A + C + y = 2 R.
…….
10) § 14 Geom:
Alle Radier ere lige store i samme Cirkel,……….
11) § 65 Geom:
Igiennem et givet Punkt A at drage en Linie AE parallel med en given Linie CD.
……
12) § 39 Geom:
Udi enhver ligebenet Triangel ABC ere Vinklerne ved Grundlinien AB lige store, A
= B.
13) § 122 Geom:
Enhver Vinkel ADB, hvis Top D er i Omkredsen af en Cirkel, har til sit Maal den
halve Bue AB, paa hvilken den staaer, eller ADB = ½ AB. ……..
14) Vexelvinkel: Ensliggende vinkler ved en linie der skærer to parallelle
linier.
15) § 60 Geom:
Naar tvende Linier AB og CD ere parallele, og skiæres af den tredie Linie HK,
saa er 1) Vexelvinklerne lige store, x = y …….
16) § 148 Geom:
Naar udi tvende Triangler ABC og DEF alle Vinklerne ere lige store, A = D, B = E
og C = F, saa ere eensbeliggende Sider i Forhold, det er:
AB : AC = DE : DF
AB : BC = DE : EF
AC : CB = DF : FE. …..
17) § 108 Geom:
Naar diameteren DE er perpendikular til Chorden AB, saa Deler den Chorden AB i
tvende lige Dele, AF = FB. ……
18) § 67 Geom:
Naar der i en Triangel ABC gives tvende Vinkler A og B, saa findes den tredje
Vinkel C ved at drage de tvende givne Vinklers Summa fra tvende rette Vinkler…..
19) § 122 Geom:
Enhver Vinkel ADB, hvis Top D er i Omkredsen af en Cirkel, har til sit Maal den
halve Bue AB, paa hvilken den staaer, eller ADB = ½ AB. ……..
20) § 20 Geom:
….har man deelt hele Cirklens Omkreds i 3600……
21) § 31 Geom:
Naar paa en Linie AB staaer den anden Linie CD, saa ere begge de jevnsides
Vinkler ACD og DCB tilsammentagne tvende rette Vinkler eller 180 Grader. ….
22) § 149 Geom:
At naar tvende Triangler blot have tvende Vinkler lige store, saa er de
ligedannede,…..
|






