Thomas Bugge: De første grunde til Regning, Geometrie, Plan-Trigonometrie og Landmaaling. 

Kiøbenhavn 1795.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

Plan Trigonometrie er den Videnskab, som lærer af trende givne Ting i en flad retlinet Triangel at beregne de øvrige trende Ting, iblandt hvilke givne Ting i det mindste maae være en Side.

Anmærkning. En Triangel kan da først bestemt beregnes, naar de trende givne Ting fuldkommen bestemme Triangelen, det er, naar de givne Ting tænkes i tvende Triangler, disse Triangler da blive lige store udi Overflade, og i de øvrige Sider og Vinkler, eller naar af de givne Ting ikkun een Triangel kan konstrueres og aftegnes. De Tilfælde, i hvilke dette skeer, ere lærte i Geometrien; saaledes bestemmes en Triangel ved tvende Sider og den indbefattede Vinkel (§.37 Geom.), ved trende Sider (§.41 Geom.); ved en Side og Vinklerne ved denne Side (§.46 Geom.); ved tvende Vinkler og en modsat Side (§.68 Geom.). Derimod en Side, en Vinkel ved denne Side, og en anden Side lige overfor samme Vinkel bestemme ei nøie en Triangel (§.68 Geom.), og deraf kan fremkomme tvende Triangler, en med en Spids, og en anden med en Stumpvinkel, hvilket bliver en trigonometrisk Tvetydighed, hvorpaa man saavel i den plane som i den sphæriske Trigonometrie har flere Exempler. Af en Triangels Overflade kan ingen af dens Sider og Vinkler udregnes, fordi man kan tænke sig utallige Triangler, som staae paa samme Grundlinie og imellem samme Paralleler, og alle ere lige store i Indhold (§.89 Geom.), men have ulige Vinkler og Sider; ligesaa lidet kan man beregne nogen af Siderne, naar blot Vinkler gives, efterdi derved ikkun fremkommer ligedannede Triangler (§.148 Geom.). Disse trende sidst nævnte Tilfælde hører altsaa ikke til Trigonometrie. Ved Plan-Geometrien kan man af de givne Ting, som bestemme Trianglen, konstruere og aftegne den (§.38.47.54 Geom.), og da ved Transportør ¹⁾ eller Maalestok udmaale og finde Størrelsen af de ukiendte Vinkler og Sider; alt dette kan dog ikkun skee med den Grad af Nøiagtighed, og med den Vished, som Transportørens og Maalestokkens Strørrelse ville tillade, og er langt fra ei tilstrækkelig udi saa store Triangler, som fremkomme udi geografisk Landmaaling, i Navigation, i Astronomie og Geographie, hvor Trigonometrie, hvilken ei ved Konstruktion, men ved Beregning bestemme de søgte Vinkler og Sider, er gandske uundværlig.

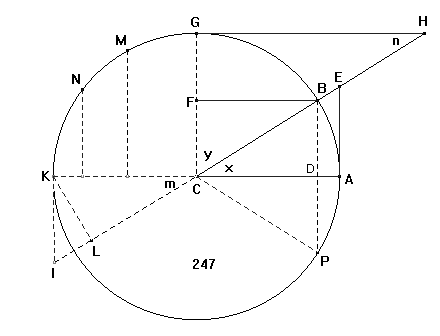
    Sinus til en Bue AB eller en Vinkel x er en Perpendikular ²⁾ BD, som drages fra den ene Ende B af Buen til den Radius AC, som drages igiennem den anden Ende A. Heraf følger: 1) Naar Buen er ingen eller = 0, eller naar B falder ind med A, kan der ei heller blive nogen Perpendikular BD, eller Sinus er ogsaa = 0; 2) Sinus voxer fra 0⁰ til 90⁰, fordi BD bliver større og større; 3) Naar Buen AB var 90⁰ eller B faldt ind med G; da falder Perpendikularen CG i Centeret C. Paa den anden Side, saasom i M og N bliver Sinus igien mindre, indtil den udi K eller 180⁰ igien er = 0, hvoraf sees, at Sinus til en Bue paa 90⁰ eller Sinus til en ret Vinkel er saa stor som Radius, og den største af alle Senuser, hvorfor den og kaldes Sinus Totus, hvilken derfor herefter skal betegnes med R eller sin.tot. 4.) Sinus BD til en given Bue AB er den halve Chorde ³⁾ = ½ BP af en Bue BAP, som er dobbelt saa stor. Man tager en bue AP = AB; man drager en Chorde BP; og fra Centeret C drages til Chorden Perpendikularen CD, saa skierer denne baade Chorden BP og Buen BAP i tvende lige Dele, eller BD = ½ BP; og x = AB = ½ BAP (§.108 Geom.⁴⁾ ); men BD er Sinus til AB, altsaa er Sinus til AB = ½ BAP lige stor med den halve Chorde = BD = ½ BP af en Bue, som er dobbelt saa stor; 5.) Sinus BD til en Bue AB eller en Vinkel x paa 30⁰ er den halve Radius = ½ AC; thi Sinus til 30⁰ er den halve Chorde = ½ BP til 60⁰ ; men Chorden BP til 60⁰ = Radius (§.170 Geom.⁵⁾ ); derfor Sinus til 30⁰ = ½ Radius = ½ AC.

Fig.247.
    Cosinus til en Bue AB eller Vinkel x er Stykket CD af Radius AC fra Sinus BD til Centret C. heraf følger 1). Naar Buen var ingen = 0 og B faldt sammen med A; saa faldt og D ind med A; eller naar Buen = 0, er Cosinus saa stor som Radius. 2.) altsom Buen AB voxer, bliver Cosinus CD mindre og mindre, og endeligen naar Buen er 90⁰ , hvis Sinus = GC (§2), bliver Cosinus ingen. 3.) Af tvende Buer AB og BG, eller af tvende Vinkler x og y, hvilke tilsammen udgiøre 90⁰, siges den ene at være den andens Complement; saaledes er y Complementet til x. Naar man fra B drager BF perpendikular til Radius CG; saa bliver FD et Parallelogram, hvor CD = FB, og BD = CF (§.74 Geom. ⁶⁾ ); men FB er Sinus og FC er Cosinus til Buen GB eller Vinkelen y (§.2); altsaa er den Linie CD, som er Cosinus til en given Bue AB, tillige Sinus til en Bue GB, som er Complementet til AB, eller Cosinus er det samme som Sinus til Complementet.

Fig.247.
    En Tangens til en Bue AB eller en Vinkel x er det Stykke AE af en Perpendikular til Radius AC, som afskiæres i E ved den anden forlængede Radius CB. Heraf følger: 1.) At naar Buen er ingen eller = 0, er og dens Tangens = 0: 2.) fra 0⁰ til 90⁰ bliver Tangens større og større; men Tangens til 90⁰ = AG er uendeligen stor; thi da AE i dette Tilfælde bliver parallel med CG (§.59 Geom.⁷⁾ ), saa maae de overalt staae lige langt fra hinanden og kan aldrig skiere hinanden, (§.61 Geom.⁸⁾ ); altsaa er AE større end enhver endelig Størrelse, og uendelig stor, (§.22 Arith.⁹⁾). 3.) Tangens AE til 45⁰ er saa stor som Radius AC; thi naar Buen AB = x = 45⁰ , saa bliver den retvinklede Triangel CAE en ligebenet Triangel, og AE = AC (§. 55 Geom. ¹⁰⁾ ). Cotangens til en Bue AB eller Vinkel x er Linien GH, som er Tangens til dens Komplement BG eller y. Naar Buen er = 90, er Cotangens = 0 ; Cotangens voxer, naar Buen tager af; og endeligen naar Buen = 0, er Cotangens uendelig stor, fordi GH og AC ere parallele (§.61 Geom.⁸⁾).

Fig.247.
    Secans til Buen AB eller en Vinkel x er Hypothenusen CE i en retvinklet Triangel CAE, hvis Catheter er Radius AC og Tangens AE; Cosecans er Hypothenusen CH i en Triangel, hvis Catheter ere Radius CG og Cotangens GH; Sinus Versus er Stykket AD fra Enden af Radius A til D, hvor Sinus BD støder paa Radius. Cosinus Versus er Stykket GF fra Enden af Radius G til Cosinus FB.

_______________________________________________________________________________

0) Bemærkning til definitionen af sinus til en bue:
På den måde sinus til en bue AB defineres afhænger sin(C) af radius R = AC. I stedet for sin(C) burde man skrive sin _R (C) for at vise hvilken radius der tænkes på. Sin _R (C) svarer da til RH sin(C) med vores betegnelser. Af de ensvinklede trekanter på figuren nedenfor ses at sin _R (C) = RH sin(C) .

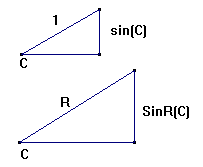
 Man kan derfor erstatte sin _R (C) / R med sin(C) / 1. Bemærk at denne omskrivning
bliver brugt i mange udregninger i § 13-19 uden at der bliver gjort opmærksom på det. Grunden til at man gør det er at sinustabellerne man brugte svarede til radius lig med 1.
Ligesom ved sin kan tang _R (C) / R erstattes med tang(C) / 1.
1) Tansportør: Vinkelmåler.
2) Perpendikular : en linie der står vinkelret på en anden linje.
3) Chorde: En korde er et liniestykke der forbinder to punkter på cirkelperiferien.
4) § 108 Geom: Naar Diameteren DE er Perpendikular til Chorden AB, saa deler den Chorden AB i tvende lige Dele, AF = FB. …….
5) § 170 Geom: Polygon-Siden AB i en regulair Sexkant ABDEFG er saa stor som Radius AC til den uden om Polygonen skrevne Cirkel.
6) § 74 Geom: Naar en firkantet Figur ABCD er et Parallelogram, og man drager Diagonalen AC, saa deeler Diagonalen Parallelogrammet i tvende lige store Triangler ACD = ACB; og Parallelogrammets modsatte Sider og Vinkler ere lige store, AD = BC, AB = DC, B = D, og A = C. …….
7) § 59 Geom: Naar paa en given Linie AB drages tvende Perpendikularer AC og BD, beliggende i samme Flade, saa kaldes AC og BD parallelle Linier …..
8) § 61 Geom: Parallelle Linier AB og CD staae overalt lige langt fra hinanden, og i hvor langt de end forlænges, kan de aldrig løbe sammen.
9) § 22 Arith: ……. En ganske anden Sag er det, naar en endelig Størrelse divideres med Nul F.eks. 8/0. Qvotienten maatte da være en saadan Størrelse, i hvilken Enheden indeholdes saa mange gange, som divisor 0 i Dividendus 8 ¹¹⁾. (§.20). Lad os nu tænke os Nul, ei som et fuldkomment Nul, men som en uendelig liden Størrelse, F.Ex. en Qvadrillion-Deel ¹²⁾ , saa matte man tage en forfærdelig stor Mængde af disse Qvadrillion Dele, forinden man kunde erholde Tallet 8; saaledes maatte man tage en uendelig stor Mængde af Enheder, for at frembringe Qvotienten, det er Qvotienten ville blive uendelig stor. Endelige Størrelser ere de, som have en bestemt Mængde af Enheder. En uendelig stor Størrelse er den, som er større end enhver endelig Størrelse. En uendelig lille Størrelse er den, som er mindre end enhver endelig Størrelse.
10) § 55 Geom: Når i en Triangel ABC Vinklerne ved Grundlinien ere lige store, A = B, saa er Trianglen ligebenet AC = CB. ……
11) Dividendus: Dividend er det tal er skal deles med et andet tal ved division.
12) Qvadrillion: Kvadrillion er en billion billioner lig 10 ²⁴.