Thomas Bugge: De første grunde til Regning, Geometrie, Plan-Trigonometrie og Landmaaling. 

Kiøbenhavn 1795.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

Tab.16.
Fig.253.

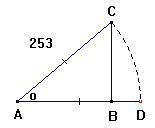
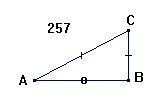
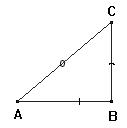
Naar der i en retvinklet Triangel ABC gives Hypothenusen AC, og en af de spidse Vinkler A, da findes den Side CB, som staaer lige over for den spidse Vinkel A ved følgende Forhold: som Sinus totus til Hypothenusen AC, saaledes Sinus af den spidse Vinkel A til den modstaaende Side CB, eller
            R : AC = sin.A : CB.⁰⁾

Man antager AC som Radius, og fra A som Center beskriver man Buen CD, og forlænger AB til D, saa er AC = R = sin.tot. og CB = sin.A (§.2); altsaa R : AC = sin.A : CB
f.Ex. AC = 2360 Alen ¹⁾ A = 34⁰.20´. ^{2)
                                  3)} Log.2360 = 3.3729120
                      Log.sin.34⁰ 20 = 9.7512842
                                               13.1241962
                           Log.sin.tot. = 10.0000000
                                Log.CB = 3.1241962
                                       CB = 1331,5 Alen

§. 14.

Naar i en retvinklet Triangel ABC gives Hypothenusen AC, og en af Catheterne AB, da findes den Vinkel A, som ligger ved denne Cathet, ved følgende Forhold: Som AC til AB saaledes Sinus Totus til Cosinus af A, eller
                 AC : AB = sin.tot. : cos.A.

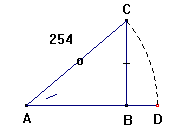
Naar man fra A som Center slaaer Buen CD med Radius AC, saa er AC = R = sin.tot.; og AB = cos.A (§.3); altsaa AC : AB = R : cos.A.

      F.Ex. AC = 4000 Alen; AB = 2000 Alen.
                       Log.Sin.Tot. = 10.0000000
                           Log.2000 = 3.3010300
                                             13.3010300
                            Log.4000 = 3.6020600
                          Log.Cos.A = 9.6989700
                                        A = 60⁰.

§ .15.

Naar i en retvinklet Triangel gives en spids Vinkel A, og den lige over for staaende Cathet BC, da findes Hypothenusen AC ved følgende Forhold: Som Sinus af A til BC, saaledes Sinus Totus til Hypothenusen AC, eller
               sin.A : BC = R : AC.

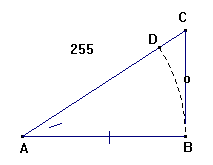
Beviset er klart af §.13, af hvilken denne Forhold ikkun er en anden Omsætning.
    F.Ex. BC = 4524 Alen; A = 54⁰ 20´
                              Sin.Tot. = 10.0000000
                           Log.4524 = 3.6555226
                                             13.6555236
                    Log.Sin.54⁰ 20´= 9.9097821
                               Log.AC = 3.7457405
                                      AC = 5568,6 Alen.

§.16.

Naar en af Catheterne AB og den ved samme liggende spidse Vinkel A gives, da findes den anden Cathet BC ved følgende Forhold: Som Sinus Totus til Tangens af A, saaledes AB til BC, eller R : Tang.A = AB : BC.

Af A som Center med Radius AB beskrives en Bue, saa er AB = R = sin.tot.; og BC = Tang.A (§.4); altsaa R : Tang.A = AB : BC. ⁶⁾
    F.Ex. AB = 46836 Alen; A = 41⁰ 40´ 20´´
                    Log.Tang. 41⁰ 40´ 20´´ = 9.9494379
                                       Log.46836 = 4.6705798
                                            Log.BC = 4.6200177
                                                   BC = 41688,6 Alen

§.17.

Naar begge Catheterne AB og BC gives, da findes den spidse Vinkel A ved følgende Forhold:
som AB til BC, saaledes Sinus Totus til Tangens A, eller
AB : BC = R : Tang.A.

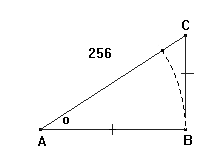
Denne Sætning er den omvendte af den foregaaende (§.16).
    F.Ex. AB = 500 Fod; BC = 896 Fod.
                           Log.Sin.Tot = 10.0000000
                                Log.896 = 2.9523080
                                                12.9523080
                                Log.500 = 2.6989700
                           Log.Tang.A = 10.2533280
                                           A = 60⁰ 40´ 13´´ ⁷⁾

§.18.

Tab.17.
Fig.257.

Naar i en retvinklet Triangel gives Hypothenusen AC og den ene Cathet BC, at finde den anden Cathet AB.
    1. Man søger Vinkelen A ved følgende Forhold: AC : R = CB : sin.A (§.12.15).
    2. Naar man saaledes har fundet Vinkelen A, søges AB ved følgende Forhold: 
R : cos.A = AC :AB (§.15).
    F. Ex. AC = 6250 Alen, BC = 1240 Alen.
                                    AC : R = CB : sin.A
                                  6250 : R = 1240 : sin.A
                               Log.sin.tot. = 10.0000000
                                 Log.1240 = 3.0934217
                                                   13.0934217
                                 Log.6250 = 3.7958800
                                 Log.sin.A = 9.2975417
                                             A = 11⁰ 26´ 36´´
                 Fremdeles R : cos.A = AC : AB
                 R : cos.11⁰ 26´ 37´´ = 6250 : AB
                                  Log.6250 = 3.7958800
                          cos.11⁰ 26´ 37 = 9.9912803
                                     Log.AB = 3.7871603
                                            AB = 6125,8 Alen. ⁸⁾

§.19.

 Naar i en retvinklet Triangel gives begge Catheterne AB og BC, at finde Hypothenusen AC.
    1. Man søger Vinkelen A ved følgende Forhold, AB : BC = R : tang.A (§.17).
    2. Naar man har fundet Vinkelen A, findes Hypothenusen ved følgende Forhold: sin.A : BC = R : AC (§.15).
    F.Ex., AB = 300 Fod; BC = 400 Fod
                                AB : BC = R : tang.A
                              300 : 400 = R : tang.A
                  Log.400 + Log.R = 12.6020600
                                Log.300 = 2.4771213
                            Log.tang.A = 10.1249387
                                          A = 52⁰.7´.48´´
                             sin.A : BC = R : AC
              sin.53⁰.7´.50´´ : 400 = R : AC
                         Log.400 + R = 12.6020600
                     Log.sin.53.7.48 = 9.9030894
                                 Log.AC = 2.6989706
                                        AC = 500 Fod. ⁹⁾

Anmærkning. Dette sidste Probleme kan ved Geometrie opløses; thi AC² = AB² + BC² (§.93 Geom.¹⁰⁾), og AC = ; og i det givne Exempel AC = = = 500. Det nest foregaaende Probleme (§.18) kan og opløses efter den Pythagoræiske Læresætning; og AB = , hvilket Udtryk kan opløses ved Logarithmer, naar man forudsætter det, som siden i Bogstavregningen (§.8 Algr.) skal bevises, at AC² - BC² = (AC + BC)(AC - BC); thi da bliver AB udtrykt ved Logarihtmer, eller log.AB = (log.(AC + BC) + log.(AC-BC)) / 2 (§.113 Arith. ¹¹⁾). Det i §.18 anførte Exempel vil da efter denne Regningsmaade saaledes udfalde:
                          AC = 6250                      AC = 6250
                          BC = 1240                       BC = 1240
                AC + BC = 7490             AC - BC = 5010
          log.(AC + BC) = log.7490 = 3.8744818
           log.(AC - BC) = log.5010 = 3.6998377
       log.(AC² - BC²) = log.( 7490H 5010 ) = 7.5743195
  log.AB = ½ l.(AC² - BC²) = ½ l.( 7450H 5010) = 3.7871598
                   AB = 6125,7 ¹²⁾
Den ubetydelige Forskiel, som findes imellem denne Logarithme og Logarithmen i §.18, har sin Oprindelse af Uvisheden i Logarithmernes sidste Decimal; og om man ville have den nøiere, da maae man bruge Logarithmer med flere Decimaler (§.112 Arith.)

§. 20.

Disse Problemer ere Grunden til alle retvinklede Trianglers Opløsninger, hvilken ved de givne Exempler tilstrekkeligen ere oplyste. Alle muelige Tilfælde, hvilke kan indtreffe ved retvinklede Triangler, ere i alt 21, og indbefattes i følgende Tavle, hvortil hører en af Figurerne fra 252 til 258.

0) Bemærk at R / AC = sin _R(A) / CB kan omskrives til sin _R (A) / R = CB / AC.
    Derfor kan man uden fejl (se §2 kommentar) sætte R = 1 og dermed CB = sin(A) H AC / 1.
    Dette gøres i udregningen uden kommentar, idet man sætter sin.tot. = R = 1 og log.sin.tot =
1) Målestoksforhold:
   1 Fod = 10 decimaltommer = 100 decimallinier = ½ Alen. 1 Alen = 62.8 cm.
2) Vinkelmål :
    En hel cirkel deles i 360⁰.
    Hver grad deles i 60 bueminutter ( skrives 60´) og hvert bueminut deles i 60 buesekunder (skrives 60´´).
   F.eks. betyder 20⁰ 13´45 ´´ : 20 grader, 13 minutter og 45 sekunder
   Eksempel på omregning:
           20⁰ 13´ 45´´ = 20 + 13 / 60 + 45 / 60² = 20.2291667⁰.
   Tilbageskrivningen 20.2291667⁰ ser sådan ud:
           20.2291667 - 20 = 0.2291667 (træk heltalsværdien fra)
           0.2291667H 60 = 13.75000 (multiplicer med 60)
           13.75000 - 13 = 0.7500 (træk heltalsværdien fra)
           0.7500 H 60 = 45.000 (multiplicer med 60)
3) se Beregning med logaritmer.
4) § 116 Arith:
   Til trende givne Tal a, b, c at finde det fierde proportional ¹³⁾ Tal d ved Logarithmer.
     1. Man søger af Tavlerne Logarithmerne til de tvende mellemste, eller til den anden og tredje b 
   og c, og lægger disse Logarithmer tilsammen = Log.b + Log.c.
     2. Fra denne Summa drages Logarithmen af den første a; saa er det udkommende Logarithmen
   til det fierde proportional Tal d, eller Log.d = log.b + log.c - log.a. …….
5) Bemærk at R / tang _R (A) = 1 / tang (A) (se bemærkning til §2). Derfor kan man uden videre i  udregningerne sætte R = 1.
6) Log.sin.34⁰ 20´= -0.2487158 = 9.7512842 - 10
   Udregningen kan også skrives sådan:
                   Log.2360 = 3.3729120
            Log.sin.34⁰ 20 = 9.7512842 - 10
                                    13.1241962 - 10
               Log.sin.tot. = 10.0000000 -10
                    Log.CB = 3.1241962
   Log.CB = 3.1231962 fås ved "at strege 10érnes orden" i 13.1241962 ud.
7) I de sidste to linier skal der stå:
            Log.Tang.A =10.2533380
                           A = 60⁰ 50´13´´
8) I de sidste 6 linier skal der stå :
                    R : cos.11⁰ 26´ 36´´ = 6250 : AB
                                  Log.6250 = 3.795880
                  Log.cos.11⁰ 26´ 37 = 9.9912799
                                    Log.AB = 3.7871599
                                           AB = 6125,8 Alen
9)  Der skal stå:
           A = 53⁰ 7´ 48´´ og Log.400 + Log.R = 12.6020600
10) § 93 Geom:I enhver retvinklet Triangel ABC er det Qvadrat AE, som beskrives paa Hypotenusen AB, saa
   stor som begge Qvadraterne GB + AH, hvilke beskrives paa Catheterne , eller AB² = BC² + AC².      
   .........
11) § 113 Arith:
   Logarithmen til et Produkt ab findes ved at lægge Logarithmerne af begge Faktorerne a og b
   tilsammen eller Log.ab = Log.a + Log.b. ……
12) Resultatet bliver AB = 6125.757 så det burde rundes op til 6125.8. der er altså ikke nogen "ubetydelig feil".
13) Fierde proportional: I ligningen (proportionen ) a:b = c:d siges d at være fjerdeproportional til a, b, c.