ASTRONOMISK NAVIGATION -
Om kuglegeometri og koordinater på jordkloden og himmelkuglen

Download dette dokument i Word-format
Download dette dokument i pdf-format

Ivan Tafteberg Jakobsen
Århus Statsgymnasium 

Astronomisk navigation – hvad er det? 

Hvad er navigation?

Ordet stammer fra latin. ’Navis’ betyder skib, og ’ago’ er et verbum, der kan betyde mange forskellige ting, herunder at sætte i gang, lede og føre. De to ord danner tilsammen verbet ’navigare’, som så betyder at sejle eller føre et skib. Heraf kommer ordet ’navigatio’, der er det latinske substantiv for det at føre et skib.
Ordene kendes i mange forskellige sprog og i mange moderne sammenhænge – også i overført betydning. Navigatør, navy, navigate, navigator, at ’navigere’ i det moderne samfund er blot nogle eksempler. Alle har deres udspring i den kunst at kunne sejle. 

Hvorfor er dette emne interessant?

Det er i hvert fald interessant set under en historisk synsvinkel. Transport af mennesker og varer til søs kendes langt tilbage i tiden. Sejlads på Nilen i Ægypten. Sejlads på de store floder i Kina. Sejlads på Middelhavet i oldtiden. Noas ark i Det Gamle Testamente. Profeten Jonas, ligeledes fra Det Gamle Testamente, der kastes over bord og opsluges af en stor fisk. Odysseus, der efter at have deltaget i krigen mod Troja flakker omkring på Middelhavet i ti år som beskrevet i Odysséen. Fønikerne, der grundlægger handelskolonier utallige steder spredt i de landområder, der grænser op til Middelhavet. Vikingerne, der sejler fra Skandinavien ad de russiske floder til Sortehavet, plyndrer langt op ad de vesteuropæiske floder, grundlægger herskerdynastier i Normandiet og på Sicilien. Venezianerne, som i århundreder tjener formuer på at formidle handlen mellem det fjerne og det nære østen og Vesteuropa. Portugiserne og Spanierne, som baner sig vej over Atlanterhavet til Den Nye Verden, rundt om Afrika til Indien og til Kina og Japan. Og som taber kampen om magten til søs til de nordeuropæiske sømagter Holland og England. England, der etablerer et verdensomspændende imperium i kraft af sin formåen til søs.
Man kan blive ved. Myter, sagn, sømandsfortællinger, skipperskrøner og afgørende historiske begivenheder til søs er der nok at tage af. 

Men hvordan kommer matematikken ind i billedet?
Det er ikke helt lige til at forklare – især ikke kort. Der er en hel del ’mellemregninger’ man er nødt til at beherske først.

Vi vil prøve at begynde en gang i oldtiden. Lad os forestille os, at vi er ombord på skib et eller andet sted i Middelhavet.
I appendiks 1 og 2 præsenterer vi to litterære beskrivelser fra oldtiden af sådan en situation. Denne ene har karakter af sagn, den anden er formentlig stort set historisk.  

I appendiks 1 er kapitel 27 i Apostlenes gerninger citeret i sin helhed. De skildrede begivenheder foregår i det første århundrede af vor tidsregning. Her fortælles om apostlen Paulus’ sørejse fra Cæsarea (i det nuværende Israel) til Rom. Ved afrejsen fra Kreta kommer skibet ud for en storm, og der siges ”I flere dage sås hverken sol eller stjerner, og det var stadig hårdt vejr. Til sidst svandt ethvert håb om vores redning.” (v.20).
Det var åbenbart betydningsfuldt, at de ikke kunne se hverken Solen eller stjernerne. 

I appendiks 2 er vi tilbage i en langt tidligere periode, adskillige århundreder tidligere (det er ikke stedet her at diskutere fra hvilken periode de to store digte Illiaden og Odysséen stammer). Her er helten i Odysséen blevet sendt helt alene af sted på et skib fra Kalypsos ø et sted i Middelhavet. Som det fremgår havde han i høj grad sin opmærksomhed henvendt på stjernerne og stjernbillederne, ”snildt som den øvede Sømand”, og gav især agt på ’Bjørnen’, som det gjaldt om ”Stadig at have til Venstre på hele sin Fart over Havet”. ’Bjørnen’ er stjernebilledet Store Bjørn, hvis hoveddel her i landet nok er bedre kendt som Karlsvognen.
Her er det endnu tydeligere, at stjernebilledernes positioner spiller en væsentlig rolle for hvordan sømanden i Middelhavet orienterer sig, når han ikke kan se land.
Derfor taler man om astronomisk navigation.

I det følgende prøver vi at få styr på, hvordan det nu kan være. 

Hvor er vi? 

Første scenario: Vi kan se land. Vi kan se et karakteristisk bjerg, som vi har set før på en tidligere sørejse. Vi ved, at så skal vi følge kysten et stykke mod nord for at komme til en havn vi kender.
Ingen problemer. 

Andet scenario: Der er hav omkring os, så langt øjet rækker. Vi aner ikke hvor vi er, hele den foregående nat har der blæst en storm, og vi har ikke kunnet se en hånd for os. Nu er det blevet stille og det er klaret op. Solen skinner.
Den følgende nat er det stadig klart vejr, så stjernehimlen hvælver sig over os i al sin pragt.
Hvad kan vi bruge det til? 

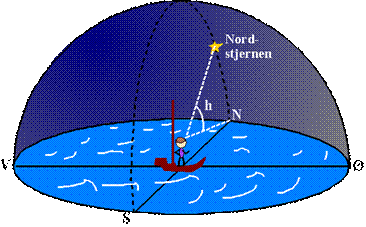
For det første Solen: 

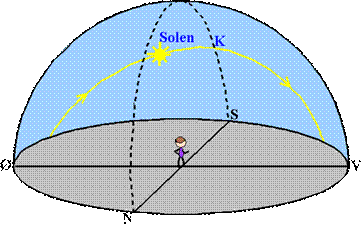
Figur 1

Solens gang hen over himmelen giver en idé om verdenshjørnerne. Den står op et sted i østlig retning og går ned et sted i vestlig retning. Der hvor den står højst på himlen (man siger at den kulminerer), er retningen mod syd. Hvis man er på den sydlige halvkugle, kulminerer Solen mod nord. 

For det andet stjernehimlen: 

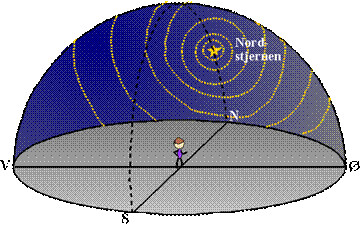
Figur 2

 I løbet af et døgn vil stjernerne foretage cirkulære bevægelser på himlen som antydet på tegningen. Man kan selvfølgelig kun se den del af cirklerne, som stjernerne beskriver mens det er mørkt. Det ser ud som om stjernerne bevæger sig omkring et punkt, der ligger fast på himlen, og meget tæt på dette punkt sidder der oven i købet en stjerne. Denne bevægelse skyldes i virkeligheden, at Jorden roterer om sig selv i løbet af et døgn omkring en akse, der peger mod dette punkt; men det var ikke opfattelsen i oldtiden, den gang mente man, at det var hele himlen der drejede omkring Jorden.
Stjernen meget tæt på omdrejningspunktet kalder man Polarstjernen (Stella Polaris), på dansk kalder man den ofte også Nordstjernen.
Nordstjernen kunne altså bruges til at fastlægge retningen mod nord med.
Foruden Nordstjernen kunne man nikke genkendende til mange andre stjerner. En del af dem havde man givet navne, og man havde ordnet mange af dem i mønstre, de såkaldte stjernebilleder. Ved iagttagelser af stjernehimlen gennem mange år og ved at tale med ældre mennesker der også havde iagttaget himlen gennem mange år, kunne man efterhånden samle så megen erfaring sammen, så man kendte stjernehimlens udseende på forskellige tider af året og vidste hvordan stjernebilledernes beliggenhed på himlen varierede i løbet af natten, og på den måde fik man en idé om hvad tid på natten det var. Man lærte, at der var nogle stjernebilleder man kun kunne se på bestemte tider af året, og andre som man kunne se hele året rundt. 

Hvis man ikke kunne se hverken land, sol eller stjerner var der meget få hjælpemidler tilbage. Kompasset dukker først op i Europa mere end tusinde år senere end Paulus levede, så den mulighed var der ikke. Så var der erfaringer om, hvilke vinde der blæste hvor og hvornår; men vejrliget var og er for lunefuldt og omskifteligt i middelhavsområdet til at disse erfaringer kunne bruges til ret meget. Endelig var der sømandens gennem år opsamlede fornemmelse for skibets hastighed og hvor langt man nok var kommet og i hvilken retning, men erfaringen viste gang på gang, at denne intuition tit slog fejl. På samme måde som det i øvrigt viste sig århundreder senere, da konservative søfolk i 1700-tallet satte større lid til deres egne fornemmelser og forældede beregninger af positionen end til det nymodens kronometer. 

Man var altså i alt væsentligt henvist til tegnene på himmelkuglen. Vi går lidt mere i detaljer med anvendelsen af Solen og Nordstjernen. 

Man havde fået erfaring for, at disse kunne benyttes ikke bare til at fastlægge verdenshjørnerne, men også til at give et fingerpeg om, hvor langt man var nord eller syd for et kendt sted.
Man havde nemlig lagt mærke til, at Nordstjernen ikke stod lige højt over horisonten alle steder. Hvis man sejlede mod nord kom den til at stå højere oppe på himlen, hvis man sejlede mod syd, lavere. Man bemærkede også, at Solen kunne komme højere op på himlen jo længere mod syd man kom. Faktisk blev denne iagttagelse udnyttet til at beregne Jordens omkreds med, idet matematikeren Eratosthenes (276-196 f.Kr.) beregnede forskellen mellem Solens højde på himlen ved sommersolhverv i Alexandria i det nordlige Ægypten og i Syene i det sydlige Ægypten (nutidens Aswân), der ligger meget tæt på den nordlige vendekreds.  

Figur 3

Figur 4

 Hvis man kan bestemme Nordstjernens højde over horisonten eller Solens højde over horisonten ved middagstid (når den står højest) har man altså et mål for hvor langt mod syd eller nord man er. Højden måles som vist på figurerne som en vinkel. 

Astronomerne havde i oldtiden instrumenter til at måle en sådan højde. Men ingen af disse instrumenter kunne bruges ombord på et skib. Det er ikke helt klart, om man havde opfundet skibsinstrumenter hertil, men sandsynligvis ikke. Muligvis brugte man mere primitive metoder til at skønne over højden, for eksempel håndsbredder på en udstrakt hånd. 

Vinkelmålingsinstrumenter er altså afgørende for, om man kan udnytte disse iagttagelser til mere præcise positionsbestemmelser. Men det ser ud som om man i oldtiden og gennem middelalderen helt op til 1300-tallet har kunnet klare sig uden sådanne instrumenter. Og det var ikke fordi man hele tiden sejlede med kysten i sigte, det viser jo de to tekster i appendiks 1 og 2.
 

Jordkloden og stedsbestemmelse 

At Jorden har form som en kugle, var allerede de græske matematikere og naturfilosoffer klar over.
Som nævnt ovenfor, bestemte Eratosthenes Jordens omkreds, og det var naturligvis på basis af den opfattelse, at Jorden er kugleformet. På samme måde mente man, at Månen, Solen og de fem dakendte planeter var bundet til kuglesfærer, der drejede sig om den ubevægelige jord. Ordet  sfære (σφαιρα) betyder netop kugle. 

De græske matematikere i oldtiden benyttede trestalssystemet (arvet fra babylonierne), når de foretog astronomiske beregninger. De inddelte cirklen  i 360 grader, og på den måde opstod det vinkelmål, der benyttes den dag i dag, hvor en såkaldt lige vinkel er en der spænder over en halvcirkel og derfor måles ved 180 grader, en ret vinkel er halvdelen af en lige vinkel og derfor måles ved 90 grader.  

I forbindelse med astronomien udviklede de græske matematikere en matematisk disciplin, der betegnes sfærisk geometri. Det betyder geometri på en kugleoverflade. Vi har brug for at kende enkelte begreber fra den sfæriske geometri: 

En storcirkel er en cirkel på en kugleoverflade, der har sit centrum beliggende i kuglens centrum. En lillecirkel er en cirkel på en kugleoverflade, der ikke har sit centrum beliggende i kuglens centrum. 

For at beskrive et steds beliggenhed på jordkloden kan vi gøre brug af disse begreber.

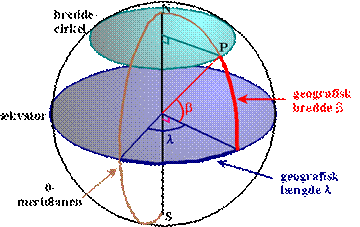
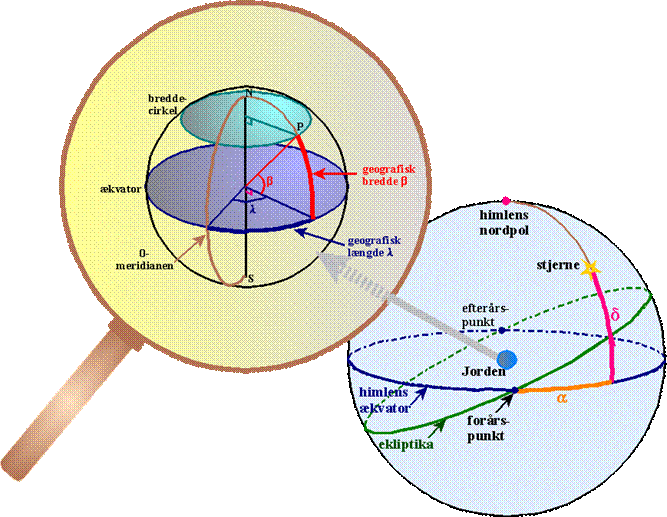
Figur 5

 Først skal vi bestemme den akse Jorden drejer sig omkring en gang i døgnet – det er den linje gennem Jordens centrum, der forbinder Nordpolen og Sydpolen. Dernæst skal vi bestemme ækvator, det er den storcirkel, der står vinkelret på jordaksen.
En meridian er defineret som en halv storcirkel, der forbinder Nordpolen med Sydpolen. Igennem ethvert sted på jordkloden går der altså en meridian. Stedets beliggenhed på meridianen fastlægges ved, hvor mange grader cirkelbuen på meridianen fra ækvator til stedet spænder over. Dette antal grader kaldes stedets geografiske bredde. Hvis stedet ligger nord for ækvator, kaldes tallet nordlig bredde, og hvis stedet ligger syd for ækvator, kaldes tallet sydlig bredde. Den geografiske bredde kan altså variere mellem 0 og 90 graders nordlig bredde og mellem 0 og 90 graders sydlig bredde. Hvis stedet ligger på ækvator, siger man at bredden er 0 grader.
Hvilken meridian stedet ligger på bestemmes således: Først fastlægges en såkaldt 0-meridian. Så måler man på ækvator, hvor mange grader man skal bevæge sig for at komme til stedets meridian. Dette antal grader kaldes stedets geografiske længde. Hvis man skal bevæge sig mod øst, kaldes dette tal østlig længde, hvis man skal bevæge sig mod vest, kaldes tallet vestlig længde. Den geografiske længde kan altså variere mellem 0 og 180 grader østlig længde og mellem 0 og 180 grader vestlig længde. Hvis stedet ligger på 0-meridianen, siger man at længden er 0. 

Punktet P på figuren har den geografiske bredde β og den geografiske længde λ. P’s bredde er nordlig bredde, og P’s længde er østlig længde.
Alle de steder på jordkloden der har den nordlige bredde β, ligger på en lillecirkel med centrum på Jordens omdrejningsakse. En sådan cirkel kaldes en breddecirkel. 

Længde og bredde er altså to tal, der tilsammen bestemmer et steds beliggenhed på Jordens overflade. På samme måde som x og y bestemmer et steds beliggenhed i et almindeligt koordinatsystem, så man kan sige at længde og bredde definerer en slags koordinatsystem på kugleoverfladen. 

Tilbage til den praktiske virkelighed.
Det var faktisk først da europæerne vovede sig ud på de store verdenshave, at de virkelig følte behovet for at bestemme deres position. Selv om middelhavssejladsen som omtalt godt kunne byde på dage uden landkending, klarede man sig åbenbart uden egentlige instrumenter. Ganske vist havde vikingerne flere hundrede år før sejlet på tværs af Atlanterhavet, men deres navigation og eventuelle brug af hjælpemidler er et kapitel for sig, som stadig er omdiskuteret og som vi ikke vil komme ind på her.  

Hvordan finder man så ud af, hvad ens geografiske længde og geografiske bredde er?
Det viser sig, at der er stor forskel på, hvor vanskeligt det er bestemme de to typer koordinater.
Den geografiske bredde bliver man tidligt i stand til at bestemme, mens bestemmelse af den geografiske længde frembyder et hårdnakket problem, der først lader sig løse i slutningen af 1700-tallet.
Så vi tager det lettere først. 

Bestemmelse af den geografiske bredde
 

Metode 1: Brug af Nordstjernen 

Som tidligere nævnt, havde man allerede i oldtiden erfaret, at jo længere nordpå man kom, jo højere stod Nordstjernen på himlen, og jo længere sydpå man kom, jo lavere stod den. Så der må jo være en forbindelse mellem den geografiske bredde og Nordstjernens placering på himmelkuglen.
Himmelkuglen er betegnelsen for den halvkugle man ser, når man står et sted på Jordens overflade og lægger nakken tilbage og ser op i himlen, plus den halvkugle under ens fødder der må være fortsættelsen af den halvkugle, man faktisk ser. Det er altså som om  man står på en flad skive, horisontplanen, og er omgivet af en kæmpestor kugle som vist på figur 6: 

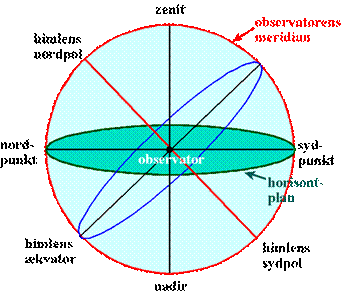
Figur 6 

Punktet lige lodret over observatørens hoved kaldes zenit, og punktet lodret under dennes fødder kaldes nadir. Bemærk, at himmelkuglen ikke er en fysisk kugle på samme måde som Jorden er det, men blot en matematisk abstraktion. Denne abstraktion  sætter os imidlertid i stand til præcist at beskrive beliggenheden af det vi ser på himmelkuglen.
Faktisk må vi opfatte himmelkuglen som en kugle med centrum lige der hvor vi står og uendelig stor radius. Det der betyder noget er retninger til punkter på himmelkuglen og vinkler på himmelkuglen og ikke himmelkuglens radius. Men når vi tegner den er vi selvfølgelig nødt til at tegne den med en bestemt radius. 

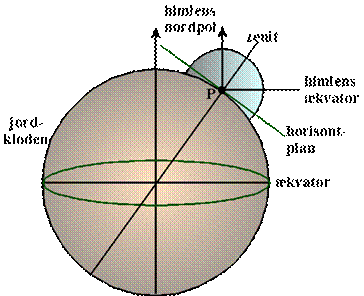
Figur 7 

I virkeligheden er horisontplanen jo tangentplan til den enorme kugle, som Jorden udgør. På figur 7 står observatøren på jordkloden i punktet P og den tegnede lille halvkugle, der ligesom er en udvækst på jordkloden, er den øverste halvdel af  himmelkuglen vist på den foregående tegning. Men bemærk venligst endnu en gang: himmelkuglen er en matematisk abstraktion, så den kunne lige så godt på figur 7 være tegnet som en 100 gange så stor kugle. Sådan en tegning kunne figur 6 egentlig godt være, hvor den store jordklode fra figur 7 så er svundet ind til den lille sorte kugle i midten af horisontplanen på figur 6. 

Når der gennem P på figur 7 tegnes en linje parallel med Jordens omdrejningsakse, fås en linje der peger i retning af himlens nordpol – det punkt på himlen om hvilket det ser ud som om alle stjernerne drejer sig i løbet af et døgn. Nordstjernen ligger meget tæt ved dette punkt, men er ikke helt sammenfaldende med det. I det følgende vil vi dog gå ud fra, at retningen til himlens nordpol og retningen til Nordstjernen er den samme. Her forudsættes det naturligvis, at Nordstjernen er så langt væk, at det ikke gør nogen målelig forskel, om man sigter mod den fra jordklodens centrum eller fra jordklodens overflade. Hvad himlens sydpol så er, giver sig selv. Linjen, der forbinder himlens sydpol og himlens nordpol kaldes undertiden for verdensaksen. Den er parallel med Jordens omdrejningsakse. Himlens ækvator er så den storcirkel på himmelkuglen der står vinkelret på  verdensaksen. Himlens ækvator ligger i en plan parallel med den plan der indeholder Jordens ækvator.
Den halve storcirkel gennem zenit og himlens nordpol og sydpol ligger i samme plan som stedets meridian på jordkloden, og den kaldes derfor også stedets meridian på himmelkuglen (observatørens meridian på figur 6). 

Nu er vi klar til at foretage breddebestemmelse, og her skal vi bruge lidt elementær geometri.
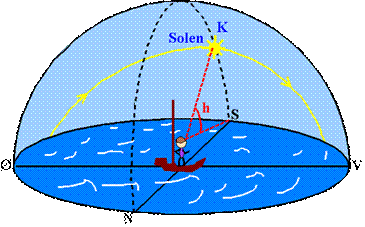
Vi kalder vinklen mellem retningen til zenit og retningen til himlens nordpol (altså Nordstjernen) for y og den mindste vinkel mellem horisonten og retningen til Nordstjernen for b (se figur 8). Vinkel b er altså Nordstjernens højde over horisonten, der kaldes h på figur 4.
Det fremgår, at y + b = 90 grader.
Linjen der forbinder Jordens centrum med P er en linje, der overskærer to parallelle linjer, nemlig de to linjer på figur 8 der begge peger mod himlens nordpol. Da ensliggende vinkler her er lige store, får man de vinkler ved Jordens centrum, der er angivet på figur 8. Men vinkel b ved Jordens centrum er jo netop stedet P’s geografiske bredde (sammenlign med figur 5). 

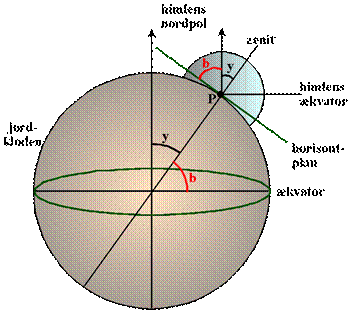
Figur 8 

Vi har nu vist, at man kan bestemme et steds geografiske bredde ved simpelthen at måle Nordstjernens højde over horisonten på det pågældende sted. Dermed har vi teoretisk løst problemet med at bestemme bredden. 

Men har vi også løst det i praksis?
Vi ser indtil videre bort fra, at Nordstjernen ikke helt ligger i himlens nordpol.
Der er i hvert fald to problemer tilbage at løse.
For det første bygger metoden jo på, at vi faktisk kan se Nordstjernen. Efterhånden som sejladsen på verdenshavene foregik længere og længere mod syd, blev det et voksende problem, at Nordstjernen rykkede tættere og tættere på horisonten og til sidst – når man passerede ækvator – forsvandt under den. Og så kunne man jo ikke bruge den til noget.
På den nordlige halvkugle, hvor man teoretisk set skulle kunne se den, kunne man i praksis komme ud for, at observationen blev umuliggjort af dårligt vejr og skydække. Det var især et problem ved sejlads i den nordlige del af Atlanterhavet.
For det andet er der problemet med i praksis at måle vinklen. Som tidligere nævnt havde man allerede i oldtiden bygget instrumenter, der kunne måle sådanne vinkler på himmelkuglen. Men de krævede fast grund og kunne ikke bruges til søs. Så hvis man skulle længere end til at skønne over vinklens størrelse i håndsbredder, måtte man opfinde instrumenter, der kunne måle vinkler til søs. Udviklingen af disse instrumenter er hænger nøje sammen med navigationens historie, og andetsteds på www.geomat.dk  kan man nærmere studere de vigtigste af dem. 

Metode 2: Brug af Solen eller en anden stjerne end Nordstjernen 

Først vil vi imidlertid se nærmere på problemet: hvad nu, hvis vi ikke kan se Nordstjernen?
Problemet lader sig ikke rigtig løse, hvis det skyldes, at himlen er overskyet. Så er der ikke andet at gøre end at vente på, at det bliver klart vejr igen.
Men vi er ikke nødvendigvis afhængige af at bruge Nordstjernen. Hvis det bliver klart vejr om dagen, kan vi simpelthen bruge Solen, og hvis det er om natten, kan vi bruge andre stjerner. I det følgende vil vi beskrive metoden under ét ved at tale om et himmellegeme. Her kan der altså være tale om både Solen og en eller anden stjerne, metoden er i begge tilfælde den samme. 

Vi får nu brug for at indføre endnu et nyt begreb: ekliptika. Ekliptika er en storcirkel på himmelkuglen som danner en vinkel på ca 23,5 grader med himlens ækvator. 

Men hvad skjuler der sig bag begrebet ekliptika?
Hvis man nøje studerer himlen gennem et helt år og noterer sig hvor Solen står i forhold til stjernerne hver dag, vil man bemærke at Solen flytter sig rundt på himlen mellem stjernerne i løbet af et år. Dens årlige bevægelse i forhold til stjernerne er en storcirkel på himmelkuglen, og det er denne cirkel man kalder ekliptika.
Ja, man kan jo ganske vist ikke se Solen og stjernerne samtidig om dagen, men så kan man notere hvilke stjerner der står diametralt modsat Solen på himlen den pågældende dag, ved at lægge mærke til hvilke stjerner der står på himlen i stik syd (’kulminerer’) den følgende nat. Det var noget man fik styr på allerede tidligt i oldtiden, og de stjernebilleder som Solen på sin årlige gang hen over himlen passerede igennem fik en særlig opmærksomhed. Man noterede sig tolv sådanne stjernebilleder, og det er de stjernebilleder, der i dag ofte betegnes ’stjernetegn’ og som tilsammen kaldes ’dyrekredsen’ eller ’zodiaken’.
Ekliptika skærer himlens ækvator to steder, som benævnes henholdsvis forårspunktet og efterårspunktet. De hedder sådan, fordi Solen befinder sig i det først punkt netop ved forårsjævndøgn og i det andet punkt ved efterårsjævndøgn.
Forårspunktet tjener nu som nulpunkt for et ’koordinatsystem’ på himmelkuglen af samme slags som geografisk længde og bredde på jordkloden. 

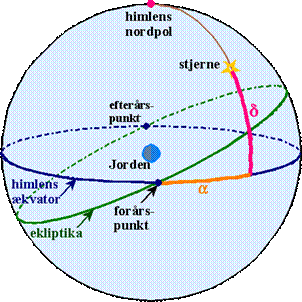
Figur 9

Et himmellegemes sted på himmelkuglen kan bestemmes ved hjælp af to vinkler, α og δ.
Et himmellegemes deklinationscirkel er den storcirkel, der går gennem himmellegemet og himlens nordpol. På figur 9 er der tegnet en fjerdedel af den. Det antal grader der måles på deklinationscirklen på det korteste stykke fra himlens ækvator til himmellegemet, kaldes himmellegemets deklination og betegnes med δ.
En deklination kan variere mellem 0 og 90 grader; hvis himmellegemet ligger nord for himlens ækvator, siges deklinationen at være nordlig eller positiv, og hvis det ligger syd for himlens ækvator, siges deklinationen at være sydlig eller negativ.
Himmellegemets rektascension α er det antal grader der måles på ækvator fra forårspunktet mod øst hen til den halvdel af himmellegemets deklinationscirkel som himmellegemet er på. Rektascensionen kan variere mellem 0 og 360 grader. 

Man siger at et himmellegeme kulminerer, når det står højest på himlen. Når det kulminerer, står det på meridianen, og det kan ske både nord og syd for zenit.. 

Hvis man nu observerer et bestemt himmellegemes højde over horisonten, når det står højest på himlen, hvordan kan man så bestemme stedets geografiske bredde?
Hertil kræves der kun kendskab til himmellegemets deklination. Dette kan indses ud fra følgende tegning: 

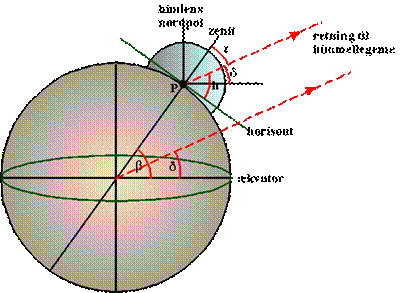
Figur 10 

Vi tænker os, at himmellegemet netop står på meridianen i syd. Himmellegemets deklination kaldes δ og dets højde over horisonten kaldes h. Vinklen mellem retningen til himmellegemet og retningen til zenit kaldes himmellegemets zenitdistance, og den er benævnt z. Så er z + h = 90 grader. Den geografiske bredde for stedet P kaldes β, og det fremgår nu af figur 10, at β = z + δ (ensliggende vinkler ved en linje der overskærer to parallelle linjer).
På figur 10 har himmellegemet nordlig deklination. Hvis det i stedet har sydlig deklination, gælder der nøjagtig det samme, blot skal δ her regnes negativ.
Man kan regne på tilsvarende måde, hvis himmellegemet kulminerer på meridianen i nord (det gør f.eks. Nordstjernen). Så skal man blot regne zenitdistancen negativ.
Vi kan derfor konkludere 

Nu er spørgsmålet selvfølgelig: Hvor får vi deklinationen fra?
Svaret er: den findes i en tabel over stjerners deklinationer og rektascensioner. Sådanne tabeller har astronomerne haft siden oldtiden, og det er ikke stedet her at komme ind på, hvordan man har fået målt eller beregnet disse størrelser. En stjerne har den samme deklination og rektascension hele tiden, da retningen til den ikke ændrer sig på himmelkuglen, men ligger fast. Det er derfor man undertiden kalder en stjerne en fixstjerne (fix = fast). Derimod har hverken Solen eller Månen eller planeterne en fast position på himmelkuglen. 

Hvis himmellegemet er Solen, er sagen altså noget mere kompliceret. Solen bevæger sig jo rundt mellem stjernerne (som tidligere nævnt er den bane den beskriver på himmelkuglen  i løbet af et år netop storcirklen ekliptika), så den skifter hele tiden deklination.
Så må man få fat i en tabel over Solens deklination på hver dag i året. Sådanne tabeller har astronomerne også haft længe. Omkring 1500 begyndte man at bringe deklinationstabeller for Solen i navigationshåndbøger (se fig.11). 

Så hvis man kan måle et himmellegemes højde over horisonten, når det kulminerer (står højest på himlen), så kan man også bestemme sin egen geografiske bredde, blot man har en deklinationstabel til rådighed for det pågældende himmellegeme.

For Danmarks vedkommende kan Solens deklination på kulminationstidspunktet aflæses for hver dag i året i Københavns Universitets Almanak, Skriv- og Rejsekalender, som udgives hvert år (se fig.12 og 13). Helt præcist er det deklinationen når Solen kulminerer på meridianen gennem Københavns Observatorium. 

Figur 11. Deklinationstabel for Solen for august måned.
Faksimile af Regimento do Estrolabio e do Quadrante,
portugisisk navigationsbog fra begyndelsen af 1500-tallet
(München, Carl Kuhn 1914)
Klik på billedet for at få stort format.

Figur 13. Tabel for august 2007 fra Almanak 2007.
 Klik på billedet for at få stort format.