|
Gradmålingsekspeditionen
til Torneådalen 1736 ved Maupertuis
Jordens
form
Flad
eller kugle
Allerede
i den antikke astronomi vidste man at jorden
havde form som en kugle. Den græske
matematiker Erasthostenes (ca. 284-192
f.Kr.) var
den første som opstillede skønsmæssige
beregninger over jordklodens størrelse. Han
observerede at i Syene (nutidens Assuan)
stod solen ved astronomisk middag ved
sommersolhverv lige i zenit, medens solen i
Alexandria danner en vinkel på 70 12´
med lodlinjen. Denne vinkel svarer til ca.
1/50 af jordens omkreds.
Erasthostenes mente at Syene og Alexandria lå
på samme meridian (hvilket ikke passer
helt) og anslog at afstanden var 5000
stadier. Det giver at jordens omkreds er
250000 stadier. Der er i dag stor usikkerhed
om hvor lang en stadie er, forskellige
kilder giver forskellige længder. En
kilde angiver 157.2 meter, det giver en
jordradius på 6255 km, det er ca. 80 km
kortere end den radius man regner med i dag.
At Erasthostenes kunne beregne jordens
radius så præcist må siges at være et
lykketræf, mange fejl og unøjagtigheder
ophævede hinanden.
Et er dog klart, beregningen bygger på
den opfattelse at jorden er rund.
Appelsin
eller Citron
Indtil
slutningen af det 17. århundrede anså man
jorden for at være en kugle.
I 1671 blev den franske videnskabsmand Jean
Ricther (1630-1696) sendt til Cayenne (i
fransk Guyena i Sydamerika lidt nord for ækvator) for at foretage
forskellige astronomiske målinger. Ved et
tilfælde opdagede han at det pendulur som
han havde justeret i Paris, tabte ca. 2 min.
i døgnet i Cayenne. For at justere uret måtte
han forkorte pendularmens længde.
Betydningen af dette blev overset indtil
Newton (1642-1727) i Principia, som udkom i 1687, gav
en forklaring på fænomenet. Newton mente
at centrifugalkraften fik jordens enorme
masse til at bule ud ved ækvator og tage
form som en appelsin.
|
Hvorfor
får jordens rotation jorden til
at bule ud?
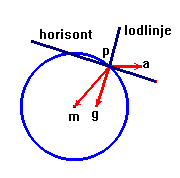
Et punkt P på jordoverfladen påvirkes
af to kræfter. Massetiltrækningskraften
m som peger ind mod jordens
centrum, og centrifugalkraften a
(på
grund af jordens rotation)
som står vinkelret på
rotationsaksen.
Tyngdekraften g, som er
summen de to kræfter a og m,
peger derfor ikke ind mod jordens
centrum.
Da tyngdekraften angiver lodlinjen
i P peger denne heller ikke ind
mod centrum.
Horisonten i P står vinkelret på
lodlinjen. Derfor er horisontens hældning
i p mindre en cirkeltantentens hældning
i P.
Jorden flader derfor ud ved
polerne.
(Se
hvorfor jorden tager form som en
ellipse).
|
 |
Tyngdekraften var derfor mindre ved ækvator
end ved polerne, hvilket forklarede
pendulurets misvisning.
Hvorfor
afhænger pendularmens længde af
tyngdekraften ?
Et penduls svingningstid T er
bestemt ved
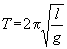
hvor
l er pendularmens længde
og g er
tyngdeaccelerationen.
Denne formel viser, at hvis hvis
man skal forkorte pendularmen for
at justere uret, må det skyldes
at tyngdeaccelerationen er mindre.
(l og g er ligefrem
proportionale).
|
Mens
Newton mente at jorden var fladtrykt ved
polerne, hævdede den franske filosof og
videnskabsmand Rene Descartes i slutningen
af 1600-tallet at jorden på grund af dens
omdrejning omkring sig selv ville være
spids ved polerne og tage form som en
citron.
Descartes opfattelse forsvaredes intensivt
af Gion Domenico Cassini (1625-1712) og
sønnen Jaques Cassini (1677-1756), som var leder ved observatoriet
i Paris. I 1701 den yngre rapporterede Cassini om en
opmåling af længden af meridianen fra
Paris til Collioure (ved den spanske grænse).
Buen som var 60 18´ blev målt
til 360.939,6 toise, hvilket giver at 10
= 57.292 toise. Cassini havde også
observeret at for hver grad man kom længere
sydpå mod ækvator tiltog længden af en
grad med 1/800, hvilket understøttede at
jorden var fladtrykt ved ækvator (se boksen
nedenfor).
Den ældre Cassini var ikke kun interesseret i jorden,
han foretog mange observationer med stjerner
og planeter. I dette arbejde opdagede han
blandt andet at Jupiter havde en betydelig
udfladning ved polerne. Det fik ham dog ikke
til at overveje om jorden havde samme form.
I følge
Newtons teori skulle 1 breddegrad ved
polerne være længere end 1 breddegrad ved
ækvator, hvis Descartes havde ret ville det
være omvendt.
Hvorfor
er breddegraderne ikke lige lange?
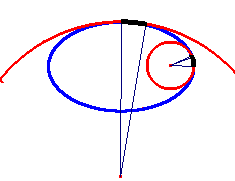
På figuren overfor ses jorden
som en ellipse der er fladtrykt
ved polerne de to røde cirkler er
tegnet så de tangerer ellipsen
ved henholdsvis nordpolen og ækvator.
Cirklen ved nordpolen vil have størst
radius. Derfor vil et cirkeludsnit
på en grad spænde over en større
bue (sort) ved polerne end ved ækvator.
Hvis jorden er flad ved ækvator,
vil det være omvendt.
(Se
også boksen : længden af en
breddegrad) |
 |
Newton og Descartes opfattelse af jordens
form var altså diametralt modsatte. I
begyndelsen af 1700-tallet var der en heftig
strid om hvem der havde ret. Det var en
strid som havde videnskabelig betydning, men
det var også en strid som havde nationale
undertoner. Var det englænderen Newton
eller franskmanden Descartes der havde ret.
For at få striden om jordens form afgjort
en gang for alle besluttede det franske
videnskabs akademi, i Ludvig XV ´s navn, at
sende en ekspedition til ækvator og en
anden til polarcirklen for at måle længden
af en breddegrad de to steder.
I 1735 drog en ekspedition, under ledelse af
la Condamine, til Quito i det daværende Peru,
nu Ecuador.
Senere samme år sendte man en tilsvarende
ekspedition, under ledelse af Maupertuis,
til Torneådalen ved polarcirklen for at måle
længden af en breddegrad der.
Resultatet
af de to ekspeditioner var at Newtons
opfattelse blev bekræftet: jorden er
fladtrykt ved polerne.
Ekspeditionen til Peru målte en bue på 30
7´3´´ til at være 176945 toises, det
giver at en bue på 10 er 56759
toises.
Ved polarcirklen måltes en bue på 57´29´´
6 til 55023 toises, det giver at en bue på
10 er 57422 toises.
Buen ved polarcirkler var altså 663 toises
(ca. 1.3 km) længere end den ved ækvator.
En
ellipsoide
I
dag er det erkendt at jorden har form som er
en ellipsoide.
En ellipsoide fremkommer ved at dreje en
ellipse 360 grader rundt om sin akse.
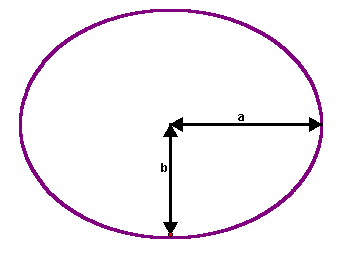
Ellipsens
fladtrykthed f er bestemt ved
f = 1 - b/a
hvor a er jordens radius ved ækvator og b
er radius ved polerne.
I dag
er radius ved ækvator bestemt til
a = 6.378,137 km
og radius ved polerne
b = 6.356,752 km,
Det giver at fladtryktheden er f = 1 :
298,257.
(Newton beregnede jordens fladtrykthed til 1
: 230)
Med
de jordradier man regner med i dag kan man
beregne længden langs meridianen fra 650
bredde til 660 bredde til 111.50
km. (650 svarer til bredden ved
Torneå)
Tilsvarende er længden fra 50
bredde til 60 bredde 110.58 km.
(50 svarer til bredden ved Peru).
Det viser at længden af en breddegrad ved
ækvator er ca. 1 km mindre end en
breddegrad ved polerne.
Se udregningerne.
|



