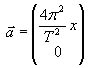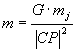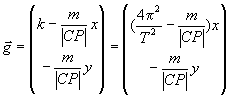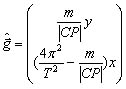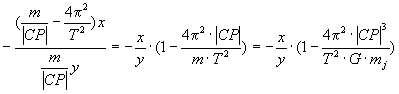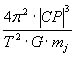Beregninger

Hvorfor bliver jordens form en ellipse?

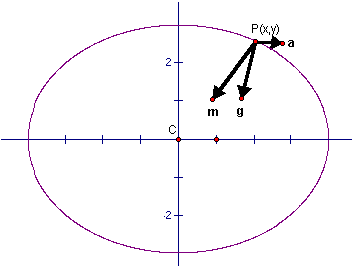
Et punkt P(x,y) på jordoverfladen påvirkes af to kræfter 
1) centrifugalkraften a:

           

(T er omløbstiden 24*60² sek og x er punktets afstand til rotationsaksen).

2) massetiltrækningskraften m:

     , 
(G = 6.672 * 10^-11 N er gravitationskonstanten og m_j = 5.974*10²⁴ kg er jordens masse).

Tyngdekraften g er lig med summen af de to vektorer g = m + a:

hvoraf fås

Tyngdekraften g bestemmer lodlinjen, som står vinkelret på horisonten. Horisontens hældning er derfor lig med hældningskoefficienten af tværvektoren til g :

Størrelsen:

afhænger kun af jordens radius CP som ændres så lidt at den i det følgende kan opfattes som konstant.
Hvis man betegner størrelsen med e² kan horisontens hældningskoefficient y´ skrives 

            y` = - x / y (1-e²).

Denne differentialligning løses ved separation af de variable:

Da kurven skal gå gennem (a , 0) hvor a er længden af radius ved ækvator er 2k = a² (1-e²)

           y² = -x²(1-e²) +a²(1-e²) y² = (a²-x²)(1-e²)

og hvis man sætter 1-e² = b² / a²  og dividerer med b² fås:

hvilket er en ellipse med de to storakser a og b. e er ellipsens extentrisitet.