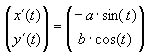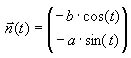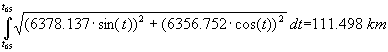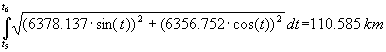Beregninger

Længden af en breddegrad.

Printervenlig udgave.

Definition af breddegrad. Jorden har form af en ellipsoide. For et punkt P på jordoverfladen defineres breddegraden som den vinkel v som en normal til ellipsens tangent i P danner med ækvator. (Vinklen v kaldes den astronomiske bredde og vinklen t kaldes den geografiske bredde).

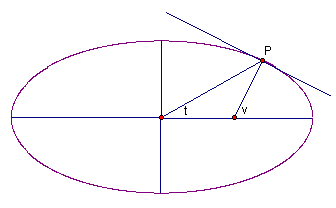
Længden af en breddegrad kan bestemmes ud fra en parameterfremstilling for ellipsen

Længden af den bue som kurvepunktet med parameterværdi t₀ bevæger sig til kurvepunktet med parameterværdi t₁ er:
              .
For at bestemme integralet må vi først bestemme parameterværdien t_v til det punkt P_v på ellipsen der har breddegrad v.
P_v er bestemt som det punkt på ellipsen, hvor linjen der står vinkelret på tangenten (horisonten) i punktet danner en vinkel på v med x-aksen (ækvator).
Hastighedsvektoren:

En normalvektor til tangenten:

Dermed har linjen der står vinkelret på tangenten hældningskoefficienten

Af tan (v) = = a / b tan(t) kan parameterværdien t_v for punktet P_v findes: 

              t_v = tan^-1(b /a tan(v))

Med de jordradier man regner med i dag, a = 6378.137 og b = 6356.752, er:

           t₆₅ = tan^-1( 6356.752 / 6378.137 tan(65) ) = 1.1331766248.
           t₆₆ = tan^-1( 6356.752 / 6378.137 tan(66) ) = 1.150667981.
           t₅    = tan^-1( 6356.752 / 6378.137 tan( 5) ) = 0.0869753462.
            t₆   = tan^-1( 6356.752 / 6378.137 tan( 6) ) = 0.104371193.

Længden af en breddegrad fra 65⁰ -bredde til 66⁰ -bredde er 
       

    
Længden af en breddegrad fra 5⁰ -bredde til 6⁰- bredde er :

De to integraler er beregnet på TI-83 ved brug af CALC-menuens 7:
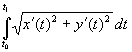