|
Gradmålingen
Gradmålingen
ved Torneå
Den
ekspedition som det franske
videnskabsakademi sendte til Torneå i
1735 havde til formål at måle længden
af en breddegrad langs medianen. (I det følgende
blot: længden af en breddegrad).
|
Hvad
betyder længden af en
breddegrad ?
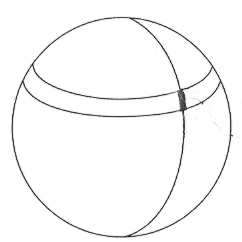
En breddeparallel er en
lillecirkel, på jordoverfladen,
der er parallel med ækvator.
Breddegraden (den geografiske
bredde) af et sted på
jordoverfladen er bestemt ved
den vinkel, som linjen gennem
stedet og jordens centrum danner
med ækvator. På figuren
overfor er vist to
breddegradsparalleller med en
grads forskel.
En storcirkel gennem polerne
kaldes en længdegradscirkel
eller en meridian. Meridianerne
står altså vinkelret på
breddeparallellerne. Ved længden af
en breddegrad forstås længden
af det markerede stykke af
meridianen.
|
|
 |
Målingen
af længden af en breddegrad ved
polarcirklen krævede mange
forskelligartede målinger og
beregninger af ekspeditionens
deltagere.
Først skulle man finde to
punkter hvis afstand langs en
meridian var ca. en grad. Som
det sydlige punkt valgte man
klokketårnet i Torneå kirke og
som det nordlige et højdedrag
ved Kittis.
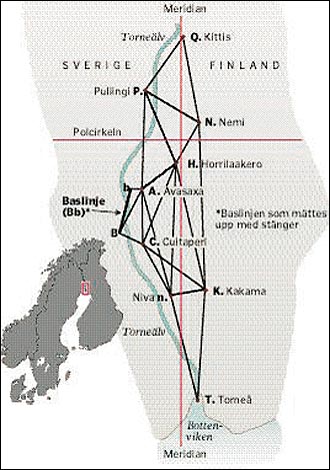
Mellem disse to punkter udlagde
man otte stationer som alle lå
på bjergtoppe langs Torneåfloden.
Disse stationer udgjorde et
trekantsnet hvor man fra alle
punkter i nettet kunne se og
sigte til alle nabopunkterne (se
kortet overfor).
I 1700-tallet var det uhyre
vanskeligt og meget omkostnings
fuldt at opmåle lange strækninger.
Derimod rådede man over
instrumenter der forholdsvis
enkelt og præcist kunne måle
vinkler.
Man målte derfor kun en eneste
linje i hele trekantsnettet.
Linjen Bb, som kaldes
basislinjen blev omhyggeligt målt
med målestok. |
Derimod
målte man vinklerne i alle trekanterne.
Ud fra basislinjens længde og vinklerne
kunne man ved trigonometriske beregninger
(svarende til sinusrelationerne) en efter
en beregne alle siderne i trekantsnettet. Først
siderne i den trekant BbA, der støder op
til basislinjen, derefter siderne i den næste
trekant ABC, osv.
Som
det fremgår af kortet ovenfor ligger
linjen mellem endepunkterne Torneå Kirke
og Kittisvaara ikke helt på en meridian.
For at kunne beregne afstanden
mellem de to endepunkter langs meridianen
måtte man først beregne længden af
trekantslinjernes projektion ind på
meridianen.
Forskellen
i breddegrad mellem de to yderpunkter i
nettet var ca. en grad. Den nøjagtige
forskel målte man ved at bestemme
stjernen Dragon vinkel med zenit i de to
endepunkter.
Endelig
målte man også breddegraden ved Torneå
ved at måle polarstjernens vinkel.
I
de følgende afsnit omtales og uddybes
alle de beregninger og målinger der er
omtalt ovenfor:
1.
Trekantsnettet fra Torneå til
Kittisvaara.
Den
sydligste station var klokkespiret ved
Torneå Kirke og den nordligste var ved et
højdedrag ved Kittisvaara. Mellem disse
to yderpunkter blev udlagt otte andre
stationer:
Niwa,
Kakama, Cuitaperi, Avafaxa,
Pullingi, Kittis, Niemi og
Horrilakero. (se mere om
stationerne i rejsen
til Torneå)
Alle stationer blev lagt på højdedrag.
Selve stationerne blev
bygget op af afbarkede træstammer
som blev sat op i en
pyramideform med en flad top.
Stationerne kunne således
bruges både til at sigte mod
fra de fra nærmeste stationer
og som platform for måleinstrumentet,
når man skulle tage sigte til
nabostationerne. Fra hver
station måltes vinklerne til
alle de nærmeste stationer med
en kvadrant med to fods radius
og forsynet med et micrometer
(se billedet overfor).
Med en kvadrant måler man skrå
vinkler (i luftlinjen) mellem to
punkter. Det var derfor nødvendigt
også at måle højdeforskellen
mellem stationerne og korrigere
de målte vinkler til
horisontale vinkler.
Se
eksempel på hvordan man
beregner en vinkels reduktion
til horisonten. |
 |
Målingerne
af vinklerne blev foretaget i hold, hvor
hver på holdet foretog individuelle målinger
af den samme vinkel. Den endelige vinkel
var middelværdien af de individuelle målinger,
som ikke afveg væsentligt fra hinanden.
De målte vinkler ses i nedenstående
tabel ( se La Figure de la terre
side 137):
|
Observerede
vinkler
|
Vinkler reduceret
til horisonten
|
Højder
|
Se
beregning af reduktion
til centrum
|
|
Fra
spiret ved Torneå Kirke
|
|
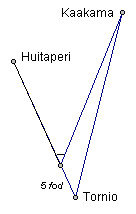
CKT
240 23´ 0´´.2
Efter reduktion fordi centeret
for instrumentet lå 5 fod fra
spiret i retning mod Cuitperi (se
overfor)
CKT…………………
KTn 19 38 20,9
Efter reduktion til centrum
KTn
|
240
22´ 58´´.8
24 22 54.5
19 38 20.1
19 38 17.8
|
N..
+ 30
K.. + 8 40
|
|
Fra
Niwa
|
|
TnK
870 44´ 24´´ 8
HnK 73 58 6.5
AnK 95 29 52.8
AnH = AnK - HnK
AnH 21 32 16.9
AnH middelværdi
CnH 31 57 5.2
|
870
44´ 19´´4
73 58 5.7
95 29 54.4
21 31 48.7
21 32 16.3
21 32 2.5
31 57 3.6
|
T -17´ 40´´
K +16´50
A
+ 4 4
H..
- 0 30
C..
+ 10 0
|
|
Fra
Kakama
|
|
TKn
72 37 20.8
CKn 45 50
46.2
HKn 89 36
0.4
HKC nKH - CKn
HKC 43 45 46.8
HKC 43 45
41.5
HKC middelværdi
CKT = CKn + nKT
HKN 9 41
48.1
|
72
37 27.8
45 50 44.2
89 36 2.4
43 45 18.2
43 45 47.0
43 45 41.7
43 45 35.7
118 28 12.0
9 41
47.7
|
n..
- 22 50
C.. - 4 45
H.. - 5 10
T.. -24 10
N.. - 8 10
|
|
Fra
Huitaperi
|
|
KCn
28 14 56.0
TKC 37 9
15.0
HCK 100 9
54.4
ACH 30 56
54.4
|
28
14 54.7
37 9
12.0
100 9 56.8
30 56 53.4
|
K..
- 6 10
n.. -19 0
H.. -2 40
A.. + 5 0
|
|
Fra
Avafaxa
|
|
HAP
530 45´
58.1
HAx 24 19
34.8
XAn 77 47
46.7
XAC 88 2
11.0
HAn = HAx + xAn
HAC = CAx + xAH
CAn 10 13
54.2
|
530
45 56.7
24 19 35.0
77 47
9.5
88 2
13.3
102 7 24.5
112 1
48.6
10 13 52.8
|
p..
+ 4´ 50´´
H..
-8 0
x.. -10 40
C.. -14 15
n.. -20 20
|
|
Fra
Pullingi
|
|
APH
31 19 53.7
QPN 87 52 9.7
NPH 37 21 58.9
|
31
19 55.5
87 52 24.3
37 22 2.1
|
H..
-22 0
A.. -18 10
Q.. -32 40
N.. -26 50
|
|
Fra
Kittis
|
|
NQP
40 14 57.3
|
40
14 52.7
|
P..
+ 22 30
N..
+ 1 0
|
|
Fra
Niemi
|
|
PNQ
57 53 13.7
PNH 93 25
8.1
HNK 27 11
55.3
|
51
53 4.3
93 25 7.5
7 1 53.3
|
P..
+18 34 0
Q.. -14 0
H.. -2 40
K..
-14 0
|
|
Fra
Horilakero
|
|
|
CHn
19 38 21.8
CHA 36 42 21.8
AHP 94 53 49.7
PHN 49 13 11.9
KHn 16 26 6.7
CHK 36 4 54.1
|
19
38 1.0
36 42
3.1
94 53 49.7
13 9.3
16 26 6.3
36 4
54.7
|
n..
-18 50
A..
0 0
P.. +11 50
N..
-5 0
K.. -12 30
C.. -10 40
|
2.
Opmåling af basislinjen fra Luppio til
Polkitorni.
Basislinjen
fra Luppio (B) til Polkitorni (b), strakte
sig over floden ved Torneå. Dette sted
var valgt fordi man her kunne måle
afstanden over isen, hvilket var meget
lettere end i et kuperet område på land.
Basislinjen blev målt med otte granstænger
af 30 fods (pied) længde. Længden af stængerne
blev omhyggeligt kontrolleret. Fra Paris
havde man medbragt en jernstang på 1
toise (ca.1.99 meter). Ved hjælp af den
lavede man en standard stang ved at slå
to søm i væggen med netop 30 fods
afstand. De otte granstænger blev
justeret efter denne standardstang, i hver
ende af de otte træstænger var et sømhoved
som blev filet væk indtil stangen havde
præcis samme længde som standardstangen.
Da man begyndte målingen lå der to fods
dyb sne på isen. Træstængerne blev lagt
på sneen i en bestemt rækkefølge. Under
hele opmålingen satte man en pæl i isen
for hver 100 toise, så man med en 50
toise lang snor hele tiden kunne
kontrollere målingerne. Hele opmålingen
af basislinjen tog ni dage fra 21. til 30.
december.
I Outhiers dagbog (side 311) kan man læse
om opmålingen af basislinjen :
December
1736 - opmålingen af basislinjen: Straks
da vi ankom til den nordlige ende af vor
base samledes vi for at begynde præcis i
signalets centrum og gå ud på isen ved
kysten i nogle få toises afstand fra
signalet. Vi delte os i to hold, hver på
fire målere. …. Vi var omhyggelige med
af mærke vore stænger, så de hele tiden
kom i samme orden, vi havde allerede målt
700 toises klokken halv to, da natten kom,
vi vendte tilbage til M.Brunius hus. Den
dag var ekstrem kold, Termometeret stod på
180 under frysepunktet. Mens i
var på basen drak M.le Monnier noget
brandy af en sølnkop, hans tunge
klistrede fast til koppen.
De to holds målinger viste næsten det
samme, der var kun en forskel på 4 Pouc
(ca.10 cm). Maupertuis mente at denne
forskel stammede fra den sidste dag hvor
man målte fra bredden op til
signalet.
I
La Figure de la terre (side 86)
angives målingerne:
Den første måling
gav 7406 toise 5 pied 0 pouse
Den anden måling 7406 toise 5 pied 4
pouse
Basislinjen bestemmes som middeltallet 7406
toise 5 pied 2 pouse.
(1
toise = 6 pied og 1 pied = 12 pouse)
Da
1 pouse svarer til 0.0277 meter er at
basislinjen er ca. 14.770 km.
3.
Beregning af de to Trekanter som begynder
alle rækkerne.
Efter
at have udlagt og målt basislinjen fra
Luppid til Polkitorni beregnede man først
siderne i den trekant ABC der stødte
op til basislinjen.
(La Figure de la terre side 86):
|
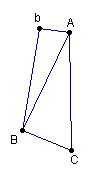
B
= Luppid
b= Polkitorni
A = Avasaksa
C = Huitaperi
|
Observerede
vinkler
|
Vinkler
korrigeret
ved beregning *) |
|
ABb
|
|
ABb
9 21´ 58´´0
AbB
77 31 48.1
BAb
93
6 7.2
179 59 53.3
|
90
22´ 0´´
77 31 50
93 6
10
180 0
0
|
|
ABC
|
|
ABC
102 42 13.5
BAC
22 37 20.6
ACB
54 40 28.8
180 0
2.9
|
102
42 12
22 37 20
54 40 28
180 0
0
|
|
*)
Hvis vinkelsummen i trekanten ikke er 180
fordeles over/underskud på de tre
vinkler, således at den største får
mest og så vinklerne bliver runde tal.
Basislinjen
blev målt til 7406 toise 5 pied 2 puose.
Ud fra denne side og vinklerne i trekant
AbB beregnede man siden AB. Videre ud frs
siden Ab og vinklerne i trekant ABC
beregnes distancen AC fra Avafaxa &
Cuitaperi til 8659.94 toises.
Eftersom de to trekanter er bestemt med
stor nøjagtighed og da deres placering er
favorabel til at bestemme denne distance
præcis, kan man betragte AC som ny
basislinje for de videre beregninger.
Se
beregning af AC.
4.
Beregninger i den første rækkes
trekanter.
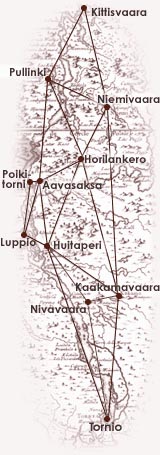
I
trekantsnettet beregnes to rækker af
trekantssider der går fra Kittis til
Torneå.
Den første række går gennem QP, PA, AC,
CT ( se figuren nedenfor).
I La
Figure de la terre (side 139) kan ses
beregning af vinklerne i de trekanter der
indgår:
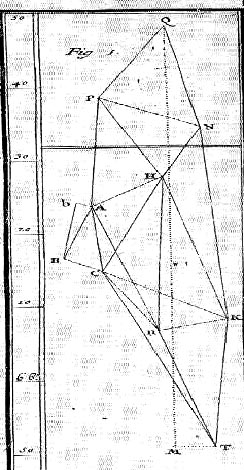 |
Observerede
vinkler,
reduceret
til horisont
|
Vinkler
korrigeret
ved beregning
|
|
ACH
|
|
CAH
1120 21´ 32´´9
ACH
30 56
53.4
AHC
36 42
3.1
180
0 29.4
|
1120
21´ 17´´
30 56
47
36 45
56
180 0
0
|
|
CHK
|
|
CHK
36 4 54.7
CKH
43 45 35.6
KCH
100 9
56.8
180 0
27.1
|
36 4
46
43 45
26
100 9
48
180 0
0
|
|
CKT
|
|
KCT
37 9
2.0
CKT
118 28 12.0
CTK
24 22 54.3
180 0
18.3
|
37 9
7
118 28 3
24 22 50
180 0
0
|
|
AHP
|
|
AHP
94 53 49.7
HAP
53 45 56.7
APH
31 19 55.5
179 59 41.9
|
94
53 56
53 46 3
31 20
1
180 0 0
|
|
HNP
|
|
HNP
93 25 7.5
NHP
49 13 9.3
HPN
37 22 2.1
180 0 18.9
|
93
25 1
49 13 3
37 21 56
180 0
0
|
|
NPQ
|
|
NPQ
87 52 24.3
NQP
40 14 52.7
PNQ
51 53 4.3
180 0
21.3
|
87
52 17
40 14 46
51 12 57
180 0
0
|
Da
AC = 8659.94 toises, som tidligere fundet,
ved hjælp af de to trekanter ABb, ABC;
finder man ved trigonometriske beregninger
i de andre trekanter siderne:
AP = 14277.43 toises
PQ = 10676.90
toises
CT = 24302.64 toises
AC = 8659.94 toises
Den
anden række der beregnes går gennem QN,
NH, HK, KT, her bestemmes siderne på
samme måde.
5.
Beregning af længden af meridianen.
De
to endestationer Torneå og Kittisvaara
ligger ikke på samme meridian.
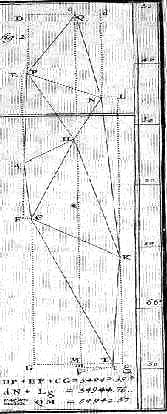
På figuren overfor er tegnet en linje QM
som er meridianen gennem Kittisvaara (Q)
med endepunkt M hvor meridianen skærer
breddegraden gennem Torneå Kirke (T). For
at beregne afstanden QM måles de vinkler
som AC, AP, PQ og CT danner med meridianen
MQ:
|
PQD
= 610 8´ 8´´
APE = 84 33 54
ACF = 81 33 26
CTG = 69 49 8
Ved
trigonometriske beregninger i
trekanterne DQP, APE, ACE, CTG
findes:
PD = 9350.45
toises
AE = 14213.24 toises
AF = 8566.08 toises
CG = 22810.62 toises
QM
= 54940.39 toises
Se
udregningen af PD.
Meridianen
udregnes gennem to rækker af
trekanter. Den anden række går
som nævnt gennem QN, NH, HK,
KT.
På figuren ovenfor er vist at
dN + Lg = QM
Beregningen af dN + Lg giver
54944.76 toises.
|
 |
Længden
af meridianlinjen QM sættes lig med
middeltallet af de to rækker ½ (54940.39
+ 54944.76 ) = 54942.57 toises
6.
Måling af forskellen i breddegrad mellem
de to yderpunkter.
Det
var ikke nok at måle længden af
meridianlinjen QM. Forskellen i
breddegrad mellem de to yderpunkter Kittis
og Torneå var ikke præcis en grad. Den nøjagtige
forskel målte man med en Zenitsector
efter en metode der stort set svarer til
den Erasthostenes brugte i år 260 e.kr.:
Metoden
går ud på at måle vinklen
mellem zenit (lodret) og en
fixstjerne, når den kulminerer
i meridianen. Denne vinkel
kaldes zenitafstanden. Når man
måler denne vinkel to steder,
vil forskellen mellem de to
vinkler være lig med forskellen
i breddegrad (se figuren
overfor).
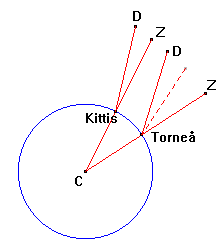
Man målte vinklen mellem Zenit
(Z) og stjernen delta-Dragon (D)
(zenitafstanden).
På figuren overfor er vinklerne
DKZ og DTZ zenitafstanden til
fixstjernen Dragon ved
henholdsvis Kittis og Torneå.
Figuren illustrerer at
forskellen i zenitafstand er lig
med forskellen i breddegrad, som
er lig med vinklen KCT, hvor C
er jordens centrum. |
 |
Bemærk
at man med denne metode ikke måler de to
steders breddegrad, kun forskellen mellem
dem.
Outhier skriver side 299:
Vi valgte stjernen delta-Dragon som den
bedst egnede stjerne for observation med
sekstanten, den passerede tæt nok på
zenit, på det mest passende tidspunkt,
for igen at blive observeret ved Torneå.
Zenitsectoren
bestod af et ni fod langt
teleskop som er fastgjort til en
jernstang, der kan drejes
vertikalt med en skrue. I den øverste
ende af jernstangen er fastgjort
en lodsnor og i den anden ende
en gradskala.
Når teleskopet drejes kan man
aflæse vinklen mellem
teleskopet og lodsnoren på
gradskalaen. Teleskopet stilles
så det kun kan dreje i
medianens retning.
Teleskopet blev indstillet så
det pegede tæt ved stjernens
kulminationspunkt. Lodsnorens
position over limben
(gradskalaen) blev aflæst.
Når stjernen dagen efter kom
til syne blev micrometeret
indstillet så lodsnorens små
forskydninger blev aflæst før
og efter at sjernen passerede trådkorset
i teleskopet. |
 |
Zenitafstanden
blev målt i Kittis og Torneå med så få
dages mellemrum som muligt (4 oktober og 1
november).
Målingerne fremgår af La Figure de la
terre, side 100:
Observationeraf
stjernen delta-Dragon, ved Kittis :
Før observationen af stjernens
meridianpassage blev lodlinjens hældning
aflæst til 20 37´ 30´´.Før
observationen aflæstes micrometeret til
24revol.
10.7 parties og
efter 24 R 12.5 p
Middeltal af de to aflæsninger er 24R
11.6p
Stjernen 22R 30.9p det
giver en difference på 1R 24.7p
(Revol.
er omdrejninger på micrometeret og
parties er dele af micrometeret på 44 per
omdrejning, 20R = 15´ ).
Samme målinger blev foretaget fire efterfølgende
dage med en gennemsnitlig difference 1R
25.8p
Observationer
af den samme stjerne ved Torneå:
Før observationen af stjernens
meridianpassage blev lodlinjens hældning
aflæst til 10 37´ 30´´.
Gennemsnitlig difference 1R
40.6p
Lodsnoren
ved passagen ved Kittis
20 37´ 30´´ - 1R 25.8p
og ved
Torneå 10 37´ 30´´ +
1R 40.6p
Det
giver forskel i zenitdistance mellem
Kittis og Torneå på 10
0´ 0´´ - 3R 22.4p
3R 22.4p er
lig med 2´ 33.8´´ som skal trækkes fra
10 0´ 0´´ hvilket giver 00
57´ 26.2´´
Dette tal underkastes tre korrektioner:
|
på grund af sektorens konstruktion |
- 0´´.65 |
|
for præsition |
- 0´´.48 |
|
for aberration |
+ 1´´.83 |
Det giver alt i alt en forskel i
breddegrad på
00 57´ 26´´.90
De samme målinger med stjernen
alfa-Dragon gav
00 57´ 30´´.35
Den
endelige forskel i breddegrad mellem
Kittis og Torneå blev fastsat som
middeltallet af de
to målinger 00 57´
28´´.63
7.
Bestemmelse af
breddegraden ved Torneå.
I
december 1736 målte man breddegraden ved
Torneå, ved at måle Polarstjernens højde
med en zenitsector.
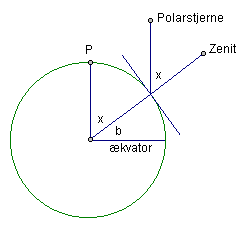 |
Hvordan
man bestemmer et punkts
breddegrad.
Polarstjernen befinder sig næsten
i himmelkuglens Nordpol, dens
bane danner en cirkel på ca. 20
.
Man kan derfor bestemme polhøjden
fra et punkt på jordoverfladen
ved at bestemme polarstjernens
nedre og øvre kulmination.
Middeltallet mellem de to
vinkler er polhøjden x fra
punktet.
Punktets breddegrad b er lig med
900 - polhøjden.
|
(La
figure de la terre side 136-137)
Nedre kulmination 220 2´ 45´´
Øvre kulmination 260
14´ 37´´
480 17´ 22´´
Der
giver middeltallet 240 8´ 41´´
som er differencen mellem Zenit ved Torneå
og Nordpolen.
Den synlige polhøjde er komplementet af
differencen 90 -240 8´
41´´= 650 51´19´´
Dette
tal skal korrigeres med refraktionen som
blev beregnet til at være 00
0´ 29´´ved Torneå .
Breddegraden ved Torneå er da 650
51´19´´ - 00 0´ 29´´ = 650
50´ 50´´.
I januar 1937 gentog man målingen af polhøjden,
denne gang med en kvadrant.
Målingerne gav at breddegraden var 650
50´ 51´´.
8.
Den endelige beregning af længden af en
breddegrad.
Efter
at have målt længden af meridianen fra
Kittisvaara til Torneå og forskellen i
breddegrad mellem de to steder kunne man
til slut beregne længden af en
breddegrad:
Længden af meridianen 54942.57 toises
Meridianbuens gradtal 00 57´28´´.63.
Det
giver at længden af en breddegrad ved
polarcirklen er 57354.15 toises (=
111.783 km)
Sammenlignet med den længde man regner
med i dag 111.498 km er den ca. 300 m for
lang.
|










