Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

 
§. 61.

Tab.21.
Fig.37.

    Paa en afstukken Linie paa Marken BCDI at oprette en perpendikular ¹⁾ Linie EFK.
    1. Med Maalebordet. Man stiller den givne Linie ab på Bordet over CI paa Marken, og a over Punktet A paa Marken (§.44). Paa Linien ab opreiser man paa Bordet en perpendikular Linie cd (§.43 og 123 Geom.²⁾⁾ . Efter denne udstikker man Linien EFK (§.53), som er den forlangte Linie perpendikular til BCDI.

Tab.21.
Fig.46.

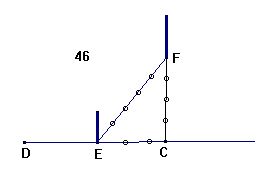
    2. Med Kieden ³).
    1. Maade. Naar i en Triangel ECF Kvadratet paa en Side EF² er saa stor som Summen af Kvadraterne paa de andre Sider EC² + CF², saa er Vinkelen ved C en ret Vinkel (§.96 Geom.⁴⁾) og FC perpendikular til EC (§.11 Geom.⁵⁾). Tallene 3,4 og 5, eller 6,8, og10 have den Egenskab, at 10² = 6² + 8² eller 100 = 36 + 64; man tager da den ene 6 te Alen af Kiæden og sætter ved en Maalepind i C, og Enden af Kiæden udspændes ved en Maalepind i Linien ved E; man tager af Kiæden CF = 8 Alen ⁶⁾ og FE = 10 Alen ( det er det øvrige af Kiæden paa 1 Alen nær): og sætter denne Ende ved den i E staaende Maale-Pind; man spænder da Kiæden ved F ud ved en Maalepind, og sætter den i Jorden, saa bliver FC perpendikular til EC.

Tab.22.
Fig.47.

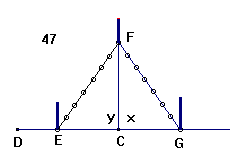
    2. Maade. Fra C maaler man til begge Sider CE = CG = 5 Alen og bemærker E og G med Maale-Pinden; ved E sættes den ene Ende af Kiæden og ved G den anden Ende; man tager Midten af Kiæden eller 12½ Alen, spænder Kiæden ud, sætter ved F en Maalepind, som bestemnmer Perpendikularen FC, thi i Î ECF og GCF er EC = CG, EF = GF, og FC = FC, altsaa x = y (§.41 Geom. ⁷⁾ ) og FC perpendikular til EG (§.11 Geom. ⁵⁾ ).

Tab.22.
Fig.51.

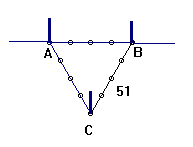
    Paa Marken at udsætte en Vinkel af 60 Grader med Kiæden. Man tager en Alen fra Kiæden, da det øvrige bliver 24 Alen, hvilke lader sig dele med 3. Ved Punktet A og i Linien AB, hvor Vinkelen skal afsættes, tager man AB = 8 Alen, og sætter den ene Ende af Kiæden ved en Maalepind i B og ved 8 Alen sættes Maalepinden i A. Enden af de øvrige 16 Alen sættes ligeledes fast ved Maalepinden B. Midten af disse 16 Alen fatter man med en tredie Maalepind; udspændes Maalepinden jevnt og den nedsættes udi C, da er Vinkelen BAC = 60^o, thi alle Siderne i Trianglen ere lige store, AB = BC = CA = 8 Alen; altsaa er Trianglen ligesidet (§.36 Geom. ⁸⁾ ), og enhver Vinkel A = B = C = 60^o (§.67.Num.5.Geom. ⁹⁾). Naar man sætter Afstiknings-Stokke i A og C, kan en Linie efter dem udstikkes; men denne Udstikning maa ikkun bruges til korte Linier, ei over 100 Alen, thi ellers vil Linien meget let kunde afvige alt for meget. Udi Fig. 38 lad AC være Stokkenes Afstand = 8 Alen. Feilen i den anden Stoks Stilling = BC = 4 Linier; thi hvem turde vel paatage, at sætte tvende Stokke i Huller af tvende Maalepinde med en mindre Feil ? AE = 100 Alen, og DE den endelige Feil i Linien; nu er AC : AE = BC : DE (§.148 Geom. ¹⁰⁾ ), og AE H BC / AC = DE; og DE = 100H 4 / 8 = 400 / 8 = 50 Linier, eller 5 Tommer. Paa 200 Alen bliver Feilen 10 Tommer, paa 300 Alen 15 Tommer o.s.v.
    Denne Feil, som kan indsnige sig ved at afsætte Vinkler med Kiæden, kan og indsnige sig ved at afsætte Perpendikularer med Kiæden, og dette er Aarsagen, hvorfor de ei maa bruges uden til korte Linier af omtrent 100 Alens Længde (§.62).

    Naar en afstukken Grundlinie eller Hovedlinie AB møder paa en Søe eller Mose, over hvilken Afstikningen vel kan foretages, men ei Kiæde- Maalingen, da at finde Længden af denne utilgiengelige Linie CF.
    For korte Distancer af omtrent 100 Alen.

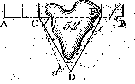
    1. Maade. Med Kiæden kan man ved Punktet C finde en Vinkel paa 60^o (§.63); Linien CD afstikker og maaler man saa langt, indtil man finder, at man i D kan komme forbi Mosen eller Søen med en Vinkel paa 60^o. Denne afsættes ved D, og Linien DF afstikkes, indtil man kommer i Linien AB ved F, da er CF = CD (§.67 Geom. ⁹⁾ ), og man begynder Maalet igien ved Punktet F.

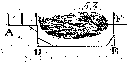
    2. Maade. Med Kiæden afsætter man ved C Perpendikularen CD (§.61), og maaler i denne Linie saa langt, indtil man i D kan komme forbi Mosen; der afsætter man DE perpendikular til CD, og forlænger den, indtil man i E er kommen forbi Mosen udi E, hvor man sætter FE perpendikular til DE, og forlænger denne, indtil man i F kommer i Linien AB. Da CDEF er et retvinklet Parallelogram (§.69 Geom.¹¹⁾ ), saa er DE = CF (§.74 Geom.¹²⁾ ), og Maalet skal begyndes fra Punktet F.
    Hvilken af disse Methoder der er den nemmeste og korteste, kommer an paa Omstændighederne. Naar Mosen eller Søen løber ud i en lang og spids Figur, som udi Figur 52, da er den ligesidede Triangel den korteste, naar Mosen er lang og smal, som udi Figur 53, saa er Rectanglet det korteste.

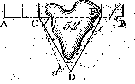
    Det er antaget, at disse ei maae bruges ved lange Distancer. Dersom man ved C afsætter en Vinkel på 60^o, saa kan man paa 100 Alen Længde meget gierne komme til et feilagtigt Punkt d, som paa 100 Alen staaer 5 Tommer fra det rette D (§.63). Naar nu igien ved d med Kiæden afsættes en Vinkel paa 60^o, saa vil man atter komme til et feilagtigt Punkt f, hvis Afstand fra det sande F vil omtrent blive 10 a`12 Tommer. Denne Feil kan endnu ansees som ubetydelig; men dersom Trianglen havde blevet større, saa have Feilen bleven mærkeligere og bør ikke taales.

2. For større Distancer over 100 Alen.
    I dette Tilfælde gaaer man enten ud med en ligesidede Triangel eller med en Rectangel; men med den Forskiel at Vinklerne maae opdrages paa Bordet og udstikkes paa Marken (§.53), og at man udi C og D tager ordentlige Stationer, Fig.52; ligeledes udi C, D, og E Fig.53 (§.58). Tilsidst bemærkes, at det let er sagt paa Papiret og i Stuen, at CD skal giøre 60^o med CF; men naar man nu i CF omtrent ved D ei kan komme til at sigte til F saa kan den Ligesidede Triangel ei bruges; og da kan man bestemme den utilgjengelige Linie CF ved enhver anden Triangel; nemlig naar man kommer til Mosen ved C, opstilles Maalebordet, og man udstikker en Linie CD i en saadan Direktion, at man et Sted i Linien f.X. i D kan komme til at sigte til Signalet eller Stokken F i Linien AB; man maaler CD, afsætter Linien CD paa Bordet og tager sigtet til F: saa har man anlagt Punktet F paa Bordet, og kan finde længden CF (§.50), og begynde Kiæde-Maalingen fra F.

__________________________________________________________________________