|
Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.
Download dette dokument i
pdf-format.
§ .49.
Efterat man saaledes har lært, hvorledes Sigter tages med
Diopter-Linealen, saa skal det dernæst undersøges, hvilke ere de Feil, som i
de maalte Vinkler kan fremkomme ved Sigter med Diopter-Linealen.
Allerførst maae det undersøges, hvor meget den allerfineste
Linie, som med Passer-Spidsen kan opdrages, udgiør. En saadan Linies Tykkelse
er sædvanligen 2/100 af en Decimal-Linie 1) = 0,0002 Fod.
Naar Stationen er taget midt paa Bordet, da er der til Kanterne i det mindste 5
Decimal-Tommer og de maalte paa Bordet aftegnede Vinkler kan man i alle
Tilfælde maale med Cirkelbuer, hvis Radius er 5 og hvis Diameter er 10
Decimaltommer eller 1 Fod. Denne Cirkels Peripherie = 3.14159 Fod (§.191 Geom.2));
og den indeholder 360H 60H
60 = 1296000 Sekunder (§.20 Geom3)). Man giør nu følgende
Forhold : 3,14159 Fod giver 1296000 Sekunder, hvad giver 0,0002 Fod eller
3,14159 : 1296000 = 0,0002 : x; man finder da x = 1296000H
0,0002 / 3,14159 = 259,2000 / 3,14159 = 82´´ 4) = 1´22´´ (§.98
Arith 5)). Dersom man havde taget den fineste Linie = 1/100 af
en Decimal-Linie (og saa fiin kan den neppe opdrages), saa havde man fundet x =
129,6000/3,14159 = 41´´. Naar man nu vil holde sig omtrent til Midten af begge
disse Bestemmelser, saa er det klart, at den fineste Linie, som man kan opdrage
paa Maalebordet, indtager i Bredde 1 Minut, og at man altsaa ved en Vinkels
Maaling paa Bordet ei tør vente at udmaale Vinkelen i finere Dele end paa 1
Minut, hvilket dog er Sandheden meget nærmere, end det er mueligt at komme den
med et Astrolabium 6) eller Boussolen 7) og
Kompasset af samme Størrelse.
§. 50.
Tab.21.
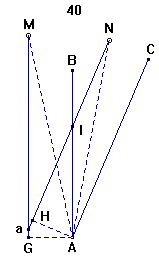
Fig.40.
Dernæst maae det undersøges, hvad Feil der kan fremkomme
i Vinklerne deraf, at Diopternes Sigtelinie gaaer igiennem Linealens Midte og
Linierne paa Bordet drages efter Linealens Kanter.
1. Lad A være Stations-Punktet paa Bordet, omkring
hvilket Linealens Kant vendes, indtil Sigtet aM igiennem Diopterne treffer
Objektet M, og man opdrager efter Linealens Kant Linien AB. Lad N være et andet
Objekt i lige Afstand fra Stationen A; man vender da Diopter- Linealen omkring
A, indtil Sigtelinien igiennem Diopterne aN treffer Objektet N, og man drager
efter Linealens Kant Linien AC. Den opdragne Vinkel paa Bordet efter Linealens
Kanter er da BAC; og den, som Sigtelinierne igiennem Diopter- Linealens Midte
have dannet, er MaN; og disse Vinkler ere lige store; thi naar Linealen er vel
verificeret, er AB parallel med aM og AC med aN (§.37 Num.2); altsaa er
Vinkelen BAC = BIN = MaN (§.60 Geom.8)). Man drager Linierne
AM og AN, saa er MaN = BAC den Vinkel, som Objekterne M og N danne seete fra
Punktet a; men MAN er den Vinkel, som Obejkterne M og N danne, naar de sees fra
Stations-Punktet A, og denne Vinkel var det, som man egentligen skulde have
opdraget paa Bordet; man drager fra A Linien AG perpendikular 10)
til aM og AH perpendikular til aN. I de retvinklede Triangler AGM og AHN ere AM
= AN, fordi man antager, at begge Objekterne ere lige langt fra Stationen A; og
AG = AH, fordi det er Diopter-Linealens halve Brede; derfor er Vinkelen M = N
(§.149 Geom.11)); af disse givne Ting kan man beregne
Vinkelen M = N; thi MG:AG = sin.tot : tang.M, (§.17 Trig.) tang.M = AGH
sin.tot / MG. Nu er AG Diopter-Linealens halve Brede = 8 Decimal-Linier = 0,08
Fod; imod hvilken AM altid er betydelig stor, saa at man kan uden mærkelig 11)
Feil tage MG = AM; naar altsaa Objektets Afstand gives fra Bordet = 15 Alen = 30
Fod = 3000 Linier, kan man beregne Vinkelen M.
log.sin.tot + log.8 = 10.9030900 12)
log.3000 = 3.4771213
log.tang.M = 7.4259687
M = 9´ 10´´
Paa denne Maade er Vinkelen M beregnet, naar Objektet er
20, 30, 50 Alen o.s.v. fra Bordet.
|
Objektets Afstand fra Bordet.
|
Vinkelen M. |
|
15 Alen
20
30
50
70
100
130
160
200
250
300
350
400
500
600
700
800
900
1000 |
9´10´´
6.51
4.35
2.45
1.57
1.23
1. 3
0.49
0.41
0.33
0.27
0.23
0.20
0.16
0.14
0.11
0.10
0. 9
0. 8 |
Ligesom man i Astronomien kalder Parallaxis den Forskiel,
som fremkommer deraf, at et Himmellegeme sees fra tvende forskiellige Steder,
f.Ex., fra Jordens Center og fra dens Overflade, saaledes kan man kalde
Diopter-Linealens Parallaxis den Vinkel M eller aMA, som kommer deraf, at man
seer til et Obejkt M en Gang fra Midten af Diopter-Linealen a og en anden Gang
fra Linealens Kant A.
Naar man nu antager Afstanden af Obejkterne M og N fra
Bordet, at være lige store, AM = AN, saa er det beviist, at M = N; men AB er
parallel med GM (§.37.Num.2); altsaa Vexel-Vinklerne 13) lige
store(§.60.Geom.8)) M = MAB; af samme Aarsag N = NAC, altsaa
MAB = NAC; disse lægges til Vinkelen BAN, saa er MAB + BAN = BAN + NAC eller
MAN = BAC; altsaa, naar tvende Objekter M og N ere lige langt fra Maalebordet,
saa bliver den efter Linealens Kanter opdragne Vinkel BAC lige stor med
Obejkternes virkelige Vinkel, havd enten Objekterne ere nær ved, eller langt
fra, Bordet; og altsaa kan det ei føre til nogen Feil, at Diopterne staae over
Midten af Linealen.
2. Dersom Objekterne ei ere lige langt borte, saa kan man
enten af Beregning eller af Tabellen udi Num.1 bestemme Vinkelen MAN; og dens
Forskiel fra BAC; f.Ex. tag AM = 50 Alen; saa er M = 2´45´´; tag AN = 100
Alen, saa er N = 1´22´´, altsaa Objekternes sande Vinkel seet fra Stationen A
eller MAN = M + BAN = 2´.45´´ + BAN; og den efter Linealens Kanter opdragne
Vinkel BAC = BAN + N = BAN + 1´22´´; altsaa naar Obejkternes Afstand er ulige
stor, bliver den egentlige Feil i den på Bordet opdragne Vinkel eller
Forskiellen imellem den virkelige Vinkel MAN og den paa Bordet opdragne Vinkel
BAC lige stor med Forskiellen imellem Vinklerne M og N = M - N; thi MAN - BAC =
M + BAN - BAN - N = M - N. I det anførte Exempel blev MAN - BAC = 2´45´´ -
1´22´´ = 1´23´´, og altsaa ei meget betydelig, naar man betænker, at den
fineste Linie paa Maalebordet allerede indtager 1 Minut. Dersom man havde taget
AM > AN, da var Feilen i Vinkelen BAC = N - M .
Af alle disse Beregninger og Betragtninger kan man
slutte at der ei i Vinklerne kan fremkomme nogen mærkelig Feil deraf, at
Diopterne staae over Midten af Diopter-Linealen .
§ 70
Tab.23.
Fig.59.

Maalebordet bliver i enhver Station stillet efter
Vaterpasset (§.43 - 44), hvis Glasrør med Flid er noget bøiet, paa det at
det ei skal blive alt for let bevægeligt, men ikkun bemærke en Helding af 3
til 4 Minuter (§.32). Lad os nu antage, at Bordet ei er stillet i den rette
horizontale Flade ACD igiennem Stationen A, men i en mod Horizonten heldende
Flade ABC; hvor stor bliver Forskiellen imellem Vinkelen BAC opdragen paa det
skievtstaaende Bord, og den Vinkel DAC, som burde være opdragen paa en
horizontal Flade?
Lad os antage et let Tilfælde, at den ene Linie AC er
Horizontal, men den anden AB over horizonten; lad den observerte Vinkel BAC i
den skraae Flade være = 60o, lad BD være en vertikal Linie; naar
man fra D til AC drager en Perpendicular DF (§.44 Geom.14)),
og ligeledes fra B til AC perpendicularen BF, saa skal de i dette Tilfælde
støde sammen i Punktet F, og Vinkelen BFD er den skraae og den horizontale
Flades Inklinations-Vinkel (§.217 Geom.15)). I den
retvinklede Triangel ABF er sin.tot. : sin.BAC = AB : BF (§.13 Trig.),
og da sin.tot. = 1 (§.12 Trig.16)); saa er 1: sin.BAC = AB :
BF; og AB H sin.BAC = BF. I samme Triangel AFB er
1: cos.BAC = AB : AF (§.14 Trig.), og AB H
cos.BAC = AF. I den ved D retvinklede Triangel BDF, er 1 : cos.BFD = BF : DF; og
BF H cos.BFD = DF; men BF = AB H
sin.BAC; altsaa AB H sin.BAC H
cos.BFD = DF. I den ved F retvinklede Triangel AFD er AF : DF = 1:tang.DAC (§.17
Trig.); og naar man indfører de forhen fundne Værdier af AF og DF, saa er
AB H cos.BAC : AB H
sin.BACH cos.BFD = 1:tang.DAC; og ved at dividere
de tvende første Leed med AB, bliver cos.BAC : sin.BAC H
cos.BFD = 1: tang.DAC (§.74 Arith.17) ) og altsaa sin.BACH
cos.BFD / cos.BAC = tang.DAC; men sin.BAC / cos.BAC = tang. BAC (§.7 Trig.):
altsaa tang.BAC H cos.BFD = tang.DAC 18)
); eller Tangenten af den til Horizonten reducerte Vinkel DAC findes ved at
multiplicere Tangenten af den observerte Vinkel BAC = 60o med Kosinus
af Bordets Inklinations-Vinkel 19) BFD.
F.Ex. BAC = 600; BFD = 40; saa er
log.tang.600 = 0.2385606
log.cos. 4 = 9.9989408
log.tang.DAC = 10.2375014
DAC = 59o.56´.23´´
|
Bordets
Hældning |
Observerte
Vinkel |
Vinkel reduc.
Til Horiziont. |
Forskiel. |
|
10
2
3
4 |
600
60
60
60 |
590.59´.46´´
59 . 59. 6
59.57.58
59. 56. 22 |
0´.14´´
0.54
2. 2
3. 38 |
Heraf seer man, at om end Maalebordet skulde have den
meget betydelige Inklination eller Hældning af en Grad, saa bliver Vinkelen i
Objekternes Plan ikkun 14´´ større end den til Horizonten reducerte Vinkel,
saadan som den burde være, om Bordet havde staaet Horizontal. Et vel indrettet
og vel justeret Vaterpas kan bemærke en hældning af 3 til 4 Minuter (§.32),
og altsaa kan de smaae Feil, hvilke kan blive tilbage i Bordets horizontale
Stilling, om det endog heldede en fierde Deel eller en halv Grad, ei frembringe
nogen mærkelig Feil udi de observerte Vinkler.
__________________________________________________________________________
Noter:
1) 1Fod = 10 decimaltommer = 100 decimallinier = ½ Alen .
1 Alen = 62,8 cm.
2) § 191 Geom:
Naar der gives en Cirkels Diameter = d, da at beregne dens Peripherie = p.
Den givne Diameter = d multipliceres med  ,
saa har man Perihperien ,
saa har man Perihperien  d; f.Ex.
Diameteren = d; f.Ex.
Diameteren =
8 Fod, saa er Peripherien = 3,141592 H 8 =
25,132736 Fod. ….
3) § 20 Geom:
…. Graden deles i 60 Minutter; og Minutter i 60 Sekunder, og 500
30´45´´ betyder 50 Grader 30 Minutter og 45 Sekunder. ….
4) Vinkelmål se 3):
En hel cirkel deles i 3600.
Hver grad deles i 60 bueminutter ( skrives 60´) og hvert bueminut deles i 60
buesekunder (skrives 60´´).
F.eks. betyder 200 13´45 ´´ : 20 grader, 13 minutter og 45
sekunder
Eksempel på omregning:
200 13´ 45´´ = 20 + 13 / 60 + 45
/ 602 = 20.22916670.
Tilbageskrivningen af 20.22916670 ser sådan ud:
20.2291667 - 20 = 0.2291667 (træk
heltalsværdien fra)
0.2291667H 60
= 13.75000 (multiplicer med 60)
13.75000 - 13 = 0.7500 (træk
heltalsværdien fra)
0.7500 H 60 = 45.000
(multiplicer med 60)
5) Til trende Tal a,b,c eller 4,6 og 20 at finde det fierde proportional Tal
d. Det andet b eller 6 multipliceres med det tredje eller 20, og Produktet bc divideres med det første a eller 4, saa er Qvotienten bc/a eller 120/4 = 30 det
søgte Tal d; …..
6) Astrolabium: Vinkelmåler. Består af en gradinddelt cirkel på hvis midte
der står en diopterlineal med nonius i begge ender.
7) Boussolen: Vinkelmåler der består af en magnetnål og en gradinddelt
metalskive.
8) § 60 Geom:
Naar tvende Linier AB og CD ere parallele og skieres af den tredje Linie HK, saa
er 1) Vexelvinklerne 9) lige store …
9) Vexelvinkler: Ensliggende vinkler ved en linie der skærer to paralelle
linier.
10) Perpendikular: En linie der står vinkelret på en anden linie.
11) § 149 Geom:
Der skulde stå § 58: Naar udi tvende retvinklede Triangler Abc og DEF gives,
at Hypotenuserne ere lige store, AC = FE, og desuden en af Katheterne lige
store, CB = FD, saa er disse Triangler i alle Måder lige store  ABC
= ABC
=  DEF…… DEF……
12) Mærkelig: Betydelig.(værd at lægge mærke til).
13) Se Beregning med logaritmer.
14) § 44 Geom:
Fra et givet Punkt C uden for en ret Linie AB at drage en perpendikular til AB
…..
15) § 217 Geom:
En Linies CD Heldning eller Inklination imod en Flade AB bestemmes ved Vinkelen
DCE, som fremkommer, naar man fra D til Fladen AB drager Perpendikularen DE, og
sammenføier C og E med en Linie…..
16) § 12 Trig:
….Siden fandt man det meget bekvemmere, at tage Radius = 1,…. Saa at sin.tot.
= R = 1 …..
17) § 74 Arith:
Naar tvende Tal 3 og 6 multipliceres med er og samme tal 5, saa er Produkterne,
som de multiplicerte Tal 3 / 6 = 3 H 5 / 6 H
5 = 15 / 30. Og naar tvende Tal 20 og 8 divideres med samme Tal 4, saa ere
Qvotienterne, som de dividerte Tal 20 : 8 = 20/4 : 8/4 = 5 : 2. …..
18) rettet fra tang.BAC + cos.BFD = tang.DAC
19) Inklinationsvinkel: vinkel mellem to planer.
|

