Beregning af højdeforskel mellem to punkter

Download i Wordformat

Download i pdf-format

Hjælpemidler:

Målebånd, teodolit, stadie, landmålerstokke.

Tekster:

Bugge § 116-118
Bugge § 129-130

Triangulering af Danmark

Beskrivelse af teodolit

Formålet med øvelsen er:

1. at få kendskab til reduktionens og refraktionens betydning ved afstandsmåling 
2. at bestemme en formel for beregning af højdeforskelle
3. at efterprøve Bugges beregning af højdeforskelle
4. at beregne højdeforskellen mellem to punkter i naturen. 

1.      Reduktionens og refraktionens betydning ved afstandsmåling:

     Spørgsmål til teksterne: Bugge § 116-118. 

1. Hvad forstår man ved den synlige horisont?

2. Hvad forstår man ved den sande horisont?

3. Hvad forstår man ved højdeforskellen mellem to punkter A og B?

4. Hvilken jordradius angives i §116, målt i km? (Sammenlign med den radius man regner med i dag)

5. Når man sigter fra et punkt A til et punkt B, hvilken retning sigter man da:
   Den sande horisont gennem A, den sande horisont gennem B, den synlige horisont gennem A eller den synlige horisont gennem B?

6. Hvad forstår man ved reduktionen ved sigte over en distance fra A til C?
   Hvad er formlen for reduktionen over en distance fra A til C?

7. Beregn reduktionen over en distance på 15000 Fod.

     Spørgsmål til teksterne: Bugge § 129-130.

8. Hvad forstår man ved refraktionen, når man sigter fra et punkt I til et punkt D?

9. Bevirker refraktionen, at man ser punktet D højere eller lavere end det i virkeligheden er fra punktet I?

10. Afstanden fra I til D er 15000 fod. Hvor mange grader (minutter - sekunder) er buen ID?
    Beregn refraktionen over en distance på 15000 fod.

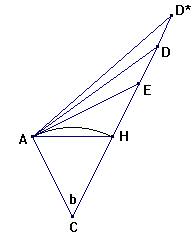
2.      Formel til beregning af højdeforskelle:

På figuren nedenfor er C jordens centrum. AH den sande horisont fra A. AE den synlige horisont fra A. AD* er sigtelinjen når man skal sigte fra A til D og man tager hensyn til refraktionen.

I §130 angives vinkel DAD*  til 1/16· b.

Når man nivellerer fra A til D måler man sigtevinklen EAD* = v.

a)      Gør rede for, at vinkel HAE = ½ b.

b)      Vis, at vinkel HAD = v + 7/16· b.

c)      Vis, at vinkel AHD = 90 +½ b.

d)      Vis, ved at bruge sinusrelationerne på trekant AHD, at:

HD = AD · sin(v + 7/16· b) / sin(90 + ½ b).

e)      Beregning af vinkel b:

Bugge angiver jordens radius til 40,673,259 Danske fod.
Omregnet giver det en jordradius på 6385702 meter. Man kan sætte AH = AD (de er jo næsten ens).

Vinkel b findes da ved at se på trekant ACH.

Når man har bestemt v og b, kan man ved formel (d) bestemme HD, som er højdeforskellen mellem A og D.

3.  Efterprøvning af Bugges beregning af højdeforskelle:

Da Thomas Bugge i slutningen af 1700-tallet lavede en triangulering Danmark,  beregnede han samtidig højdeforskellen af de observerede Stationer.

Nedenfor er et uddrag af Bugge: Beskrivelse over den Opmålingsmåde som er brugt ved de danske geografiske Karter.
Heraf fremgår, at når man sigter fra Brøndbye Høi ligger Tinghøi 8´45´´ over (den synlige) horisont. Afstanden fra Brøndbye Høi til Tinghøi (grundlinjen) er 14515 fod.

a)      Beregn på grundlag af disse oplysninger højdeforskellen mellem Tinghøj og Brøndbye Høi (brug formlen fra punkt 2).

b)      Sammenlign den fundne højdeforskel med Bugges tabel:

4.  Beregning af højdeforskellen mellem to punkter i naturen:

Vælg to punkter A og K i naturen. Der skal være en passende afstand mellem A og K (2-3 km) og en passende højdeforskel (25-100 meter). Man skal kunne sigte fra A til K. Det kan f.eks. være et kirketårn K og et punkt A ved en søkant.

Højdeforskellen mellem A og K bestemmes sådan:

a)      Vælg et punkt B ved søkanten. Afstanden fra A til B skal være 100-200 meter og man skal kunne sigte fra B til K.

b)      Mål afstanden fra A til B. Brug enten målebånd eller teodolit med stadie (eller afstandsmåler).

c)      Bestem vinklerne KAB og KBA med teodolitten (husk, at notere alle målinger omhyggeligt op).

d)      Beregn afstanden AK ved hjælp af sinusrelationerne og de i b) og c) fundne tal.

e)      Bestem den vinkel, som K ligger over den synlige horisont fra A. Brug teodolitten.

f)        Beregn højdeforskellen mellem A og K ved den formel, der er fundet i punkt 2.