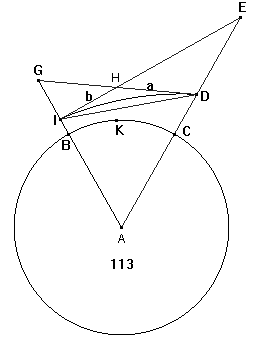
Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

§. 129.

Tab.29.
Fig.113.

    Jordkloden omringes overalt af et giennemsigtigt, tungt og elastisk flydende Legeme, som kaldes Luftkredsen eller Dunstkredsen, eller Atmosphæren, og den tilkommer den sidste Benævning, fordi alle Dampe, Dunster og Uddunstninger svømme i Luften. Luftens Tyngde foraarsager, at de nederste Lag af Luftkredsen blive mere trykkede af de oven over liggende Lag, end de Lag af Luften, som ere højere over Jorden, og da de nu ere elastiske og lade sig sammentrykke, saa maae de nederste Lag af Dunstkredsen være tættere end de øverste, saaledes at Luften maae blive tyndere og tyndere lige fra Jordens Overflade til Dunstkredsens øverste og sidste Egne. Heraf fremkommer den terrestriske eller jordiske Refraktion, ved hvilken Toppe af Bierge, Taarne og Punkter, til hvilke man i lang Afstand nivellerer, opløftes og synes høiere end de virkeligen ere. Naar I er et Sted, hvorfra man sigter eller nivellerer til et andet Sted D, da vil D ei sees efter en ret Linie eller en lige Lysstraale, hvilken vil naae Jorden, forinden den kommer til I; men en anden Lysstraale , som gaaer høiere op, og i Begyndelsen gaaer igiennem den tyndere Luft ved D, og siden ved a kommer i den tættere, vil brækkes fra sin retlinede Gang til Perpendikularen ⁰⁾ (§.124 Num.1 ¹⁾), og altsaa ned ad imod Jorden; naar den kommer lavere ned i den endnu tættere Luftkreds, vil den endnu brækkes mere fra a til b, og saaledes jo dybere Lysstraalen gaaer ned i Dunstkredsen, jo mere vil den brækkes; altsaa bliver Lysstraalens Vei fra D til I ei en ret Linie DI, men en krum Linie DabI. Øiet dømmer Objektet D at være paa det Sted E: hvilket bestemmes ved Tangenten IE til Lysets krumme Linie DabI. I den vertikale Linie vil Objektet D synes at være opløftet til E; og i Vinkel eller Cirkelbue er Vinkelen DIE den jordiske Refraktions Størrelse. Ligeledes vil man fra D see det lavere Objekt I ved den krumme Linie IbaD; Straalen gaaer ind i Øiet saaledes som om den var kommen efter Direktion af Tangenten GD; Obejktet I vil synes opløftet til G, og i høide er GI og i Vinkel er IDG den jordiske Refraktion for Objektet I.

Tab.29.
Fig.113.

Af denne givne Forklaring er det klart, at begge Objekterne D og I vil sees saaledes, som om Lysstraalerne vare komne fra begge Tangenternes Overskiærings-Punkt H, og derfra gaaet frem i rette Linier HD og HI uden Refraktion; og at Refraktionen bliver den samme, naar man antager, at Straalen var gaaet i rette Linier fra D til H; men i Punktet H paa eengang bleven brækket eller bøiet ved en Vinkel GHI = DHE (§.34 Geom.²⁾), hvilken totale Refraktion giør den samme Virkning, som alle partiale Refraktioner igiennem Lysstraalens egentlige krumme Linie DabI. Af Opmaalingerne ved man Distancen, ID, hvilken paa det nærmeste = BC; og af Gradens Størrelse = 59225 Danske Favne ³⁾ , (Opmaalingsmaaden ved de geografiske Karter §.123 til 127) eller paa det nærmeste en Fierdingvei ³⁾ lige stor med en Minut, finder man Buen BC eller Vinkelen A (§.20 Geom. ⁴⁾) i Gradmaal. Naar man nu stiller sig udi I med en geografisk Cirkel ⁵⁾ , som har en Nivellerings-Kikkert, (Opmaalings-Maade ved de geografiske Karter §.37 til 47), og observerer Objektet D, hvilket sees efter den rette Linie EI, og dets Høide-Vinkel over den synlige Horizontal-Linie igiennem I, saa erholder man Vinkelen AIE, ved at lægge 90⁰ til denne Høide-Vinkel. Ligeledes naar man staaer udi D og maaler, hvormeget I er under Horizonten af D, og man tager denne Vinklel fra 90 Grader, da ved man Vinkelen ADG. Dersom der ingen Refraktion var, saa var Punktet H og Linierne IH og HD faldet ind med ID, og alle Vinklerne udi AID = 180⁰ (§.66 Geom.⁶⁾); saa meget som A + AIE + ADG er større end 180⁰, saa meget er Refraktionens Størrelse i begge Stationer D og I, fordi IHG = HID + HDI (§.66 Geom. ⁶⁾).
    Lambert har beviist, at Lysstraalens krumme Linie DabI paa det allernærmeste er en Cirkelbue, hvis Radius er 7 til 8 Gange større end Jordens Radius AC (les proprietès remarquables de la route de la lumière, a la Haye 1759 pag.67 og 71). Bouquer troer sig ved sine Observationer at have fundet denne Radius = 9AC (Memoires de l`academie Royale des sciences de Paris 1749). Ved et Middeltal kan man tage DabI for en Cirkelbue, hvis Radius = 8AC. Paa det allernærmeste tør man tage Buerne DabI og BKC for at være af lige Længde; men i saadanne Buer forholde sig Antallet af Minuterne og Sekunderne omvendt som Radierne (§.82 Arith.), fordi jo større Radierne blive, jo større blive Minuter og Sekunder, og desto mindre er deres Antal paa samme Længde; altsaa Sekunderne udi DabI : Sekund. i CKB = AC : 8AC = 1:8 (§.74 Arith.); altsaa CKB / 8 = DabI (§.98). Refraktionens Størrelse DIE er den Vinkel, som Chorden ID giør med Tangenten IE til Lysets krumme Linie eller Cirkelbue DabI; men DIE = ½ DabI; (§.126 Geom. ⁷⁾); og DabI = 1 / 8 CKB; derfor DIE = 1 /2 H 1 / 8 CKB = 1 / 16 CKB; eller den terrestriske Refraktion er en Sextendeel af den Cirkelbue af Jorden, som indbefattes imellem det Sted, hvorfra man seer, og det Sted, hvorhen man seer. F.X. lad Afstanden imellem I og D eller BKD være 1 Miil = 4 Minut. = 240 Sekunder; saa er DIE = 240 / 16´´ = 15´´ eller Stedet D vil opløftes til, E ved en Vinkel DIE af 15 Sekunder. Professor Kramp i Strasburg har i Aaret 1800 udgivet en fortræffelig Afhandling om denne jordiske Refraction, og om den astronimiske Refraction.

Noter:
0)  Perpendikular: en linie der står vinkelret på en anden.
1)  § 124 Num.1:
1. Naar en Lysstraale AB kommer fra en tyndere Materie ind i en tættere MN, forlader den sin retlinede Gang ABC og brækkes mod Perpendikularen BE efter Linien BD, saaledes at der er et bestemt Forhold imellem Sinus af Indfalds-Vinkelen CBF og Sinus af Bræknings-Vinkelen DBE, hvilken Forhold fra Luften ind i Glas er ved et Middeltal = 3 : 2. ….
2)  § 34 Geom:
Naar tvende rette Linier AB og CD overskiere hinanden i E, saa kaldes Vinklerne x og y, samt p og q, som staae lige imod hinanden, …Topvinkler. Det skal beviises, at Topvinklerne ere lige store, x = y og p = q. ….
3)  Favn: 1 favn = 6 fod
Fierdingvei: 1/4 af en mil (ca.1.8 km)
4)  § 20 Geom:
…. For at udtrykke dette Maal med Ord, har man deelt Cirkelens Omkreds i 360 lige store Parter, som kaldes Grader. … Graden deles i 6o Minuter; og Minuter i 60 sekunder.
5)  Geografisk cirkel: Instrument der blev brugt ved triangulering af Danmark. Består af en cirkel med gradinddeling. På cirklen er fastgjort en drejelig kikkert.
6)  § 66 Geom:
Naar i enhver riangel ABC den ene Side AB forlænges til D, er den udvendige Vinkel DBC saa stor som de tvende indvendige og modstaaende Vinkler A + C, og alle Vinklerne tilsammentagne er saa store som tvende rette. …
7)  § 126 Geom:
Den vinkel DAE = x, som en Chorde AE giør med Tangenten BD, er saa stor som den halve Bue AGE, hvilken Chorden afskiærer, eller som Vinkelen i det modstaaende Segment AHFE ...