Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

Ottende Kapitel.
Om Nivellering.

§. 116.

Tab.27.
Fig.94.

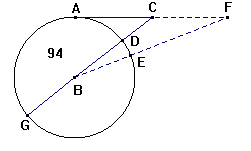
Af den mathematiske Geographie maae man her antage, som en Laanesætning, at Jordkloden er en Kugle, hvis Diameter er 40,673,259 Danske Fod ¹⁾. En sand horizontal Linie igiennem et givet Sted A er en Cirkelbue ADE beskreven fra Jordens Center B igiennem Stædet A. Den apparente eller synlige horizontale Linie igiennem Stedet A er Tangenten ACF, som berører Punktet A. 

Tab.27.
Fig.95.

At nivellere er at finde, hvor meget Stedet A ligge høiere eller lavere end Stedet B efter den sande horizontale Linie; man maae derfor igiennem A drage en sand horizontal Linie AD og igiennem B den sande horizontale Linie BE; Afstanden mellem disse Cirkelbuer AE eller BD udmaaler, hvor meget A er høiere end B, og det er Linien AE, som man ved ved Nivellering skal søge at bestemme.

Man har intet andet Middel til at bestemme langt bortværende Ting end ved de Sigter, som Lysstrålerne danne; disse gaae frem i rette Linier, saalænge Materien, hvorigiennem de gaae, er af samme Lethed; hvoraf følger, at alle Nivellerings-Sigter fra en Station A bestemme den synlige horizontal Linie ACF og ei den sande ADE. Punkterne C og F, hvilke man ved Nivellerings Sigter bestemmer, ligge ei i den sande horizontal Linie igiennem A, men over samme. Det er fornødent, at kunde reducere et Punkt C i den synlige til Punktet D i den sande horizontale Linie, eller at finde Reduktionen CD, og dette sker ved følgende Læresætning:

§ .117.

Fig.94.

Reduktionen CD fra den synlige horizontal Linie til den sande findes ved at dividere Qvadratet af den nivellerte Distance AC med Jordens Diameter DG, eller CD = AC2 / DG.

I Geometrien er det beviist, at Qvadratet paa Tangenten AC er saa stor som Rektanglet af den hele skiærende Linie og af Stykket udenfor Cirkelen (§.162 Geom. ²⁾), eller AC2 = CG H CD; nu er CG = CD + DG, de Distancer, paa hvilke man med et Slag eller et Sigte kan nivellere, overgaae aldrig ½ Miil eller 12000 Fod; og i denne Afstand er der ingen mærkelig ³⁾ Forskiel paa Buen AD og Tangenten AC; og saa meget mere bliver CD umærkelig imod Jordens Diameter DG; (DC bliver 3½ Fod og DG over 40 Millioner Fod); altsaa kan man uden mærkelig Feil endog paa de allerstørste nivellerte Distancer bortkaste CD i Sammenligning med DG, og antage CG = DG; nu var AC2 = CG HCD; altsaa og AC2 = DG H CD; og naar paa begge Sider divideres med DG, bliver AC2 / DG = CD.

§. 118.

Tab.27.
Fig. 94.

Heraf kan man nu beregne Reduktionen for enhver given Distance AC; f.Ex. 10000 Fod; nemlig AC2 / DG = CD = 100000000 / 40673259; og naar denne Regning føres ved Logaritmer ⁴⁾

                       log.100000000 = 8.0000000
                        log. 40673259 = 7.6093090
                                    log.CD = 0.3906910
                                         CD = 2,4586 Fod.

Ligesom Reduktionen CD for Distancen AC = AC2 / DG (§.116); saa er og Reduktionen FE for Distancen AF = AF2 / DG; altsaa CD : FE = AC2 /DG : AF2 / DG ; og naar man paa begge Sider multiplicerer med DG, er CD : FE = AC2 /AF2 eller Reduktionerne CD og FE forholde sig som Qvadraterne af de nivellerte Distancer. Ved Hielp af denne Sætning kan man beregne Reduktionen for enhver anden Distance, naar man lægger den allerede bestemte Reduktion for 10000 Fod til Grund; om man vil beregne for 3000 Fod, saa er AF2 : AC2 = FE : CD 100000000 : 9000000 = 100 : 9 = 2,4586 : CD; altsaa CD = 2,4586 H 9 / 100 = 22,1274 / 100 = 0,221274 = 0,2213 eller 2 Tommer 2 Linier og 1/10 Linie Decimal- Maal.

Paa denne Maade er efterfølgende Tavle beregnet, i hvilken den første Kolonne viser de nivellerte Distancer i Danske Fod, og den anden Kolonne indeholder Reduktionen i Danske Fod, Decimal-Tommer, Linier og Tiendedele Linier.