Om konstruktion af voksende kort

Download dette dokument i Word-format
Download dette dokument i pdf-format

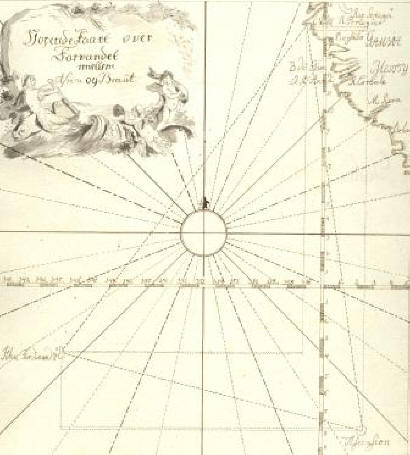
Billedet stammer fra F. Grodtschillings håndskrevne
navigationsbog fra 1795 (tilhører Orlogsmuseet).
Klik på billedet for at se det i stort format.

Det er ikke så lige til at konstruere et ”voksende kort”.
Ligesom i det ”platte kort” er alle meridianer (længdegradslinjer) parallelle med hinanden og alle breddeparalleller er parallelle med hinanden og enhver meridian står vinkelret på enhver breddeparallel.
Da meridianerne er parallelle har de overalt samme afstand, hvad de jo ikke har på jordkloden. Man kan altså ikke uden videre regne med afstande i det voksende kort.
Breddeparallellerne afsættes, så en bestemt kompaskurs overalt vil danne samme vinkel med meridianerne, dvs følge en ret linje. Som forklaret i ”Platte og voksende kort og breddecirklernes størrelse” betyder det, at afstanden mellem to på hinanden følgende breddegrader bliver større og større jo større breddegraden bliver.
Det blev faktisk vist, at ved bredden b skal afstanden mellem to breddeparalleller der ligger med f.eks. 1 bueminuts afstand
 være faktoren 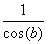 større end hvis de to breddeparalleller lå ved ækvator.

Men det fremgår jo heraf, at den faktor afstand skal ganges med afhænger af på hvilken bredde vi er, dvs faktoren ændrer sig hele tiden når vi bevæger os fra ækvator nordpå eller sydpå.
Så hvordan finder vi ud af, hvor f.eks. breddeparallellen svarende til 37 grader skal afsættes i det voksende kort i forhold til ækvator?
Dette problem løste Edward Wright (1580 – 1615) ved at dele buen på 37 grader op i mange små stykker, og så for hver enkelt stykke regne ud hvor meget afstanden skal være større end ved ækvator og derpå lægge alle disse afstande sammen. Hvis man f.eks. deler op i minutter (dvs deler i 37 ∙ 60 = 2220 små stykker) kan man finde afstanden fra ækvator til breddeparallellen som
,

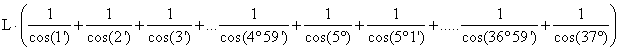hvor L er afstanden mellem to på hinanden følgende bueminutter ved ækvator, altså på en storcirkel. Denne afstand vil på kortet selvfølgelig afhænge af hvilken målestok man vælger.

Som det ses, er det et ret stort regnearbejde, der skal udføres, hvis det skal gøres nogenlunde nøjagtigt; i eksemplet ovenfor skal man regne 2220 brøker ud og derefter lægge dem samme – uden brug af lommeregner. Men det blev gjort og der blev efterhånden udarbejdet tabeller over afstandene med spring på bare 1 minut.
Omkring 1700 havde man udviklet smartere metoder, der gjorde det lettere at beregne disse tabeller, idet man gjorde brug af den såkaldte integralregning. Det vil her føre for vidt at beskrive disse metoder.

Se alle 12 sider af C. C. Lous’ ”Tabel over den voxende Brede i tiende Deel Minutter” fra 1787.