"Platte og voksende kort" og breddecirklernes størrelse

Download dette dokument i Word-format
Download dette dokument i pdf-format

For at kunne forstå bestikregning og søkort fra midten af 1600-tallet og fremefter er det nødvendigt at vide, hvad et ”plat kort” og et ”voksende kort” er for noget.  På engelsk hedder de henholdsvis ”plane chart” og ”Mercator chart” – det sidste opkaldt efter den flamske kartograf Gerardus Mercator – på latin, han hed egentlig Gerard de Kremer – (1512 – 1594). Det var ham der som den første fremstillede et kort, der benytter det der siden kom til at hedde ”Mercator-projektionen”. Det var dog englænderen Edward Wright (1580 – 1615), som formulerede den matematiske basis. 

I det følgende trækker vi på to kilder fra slutningen af 1700-tallet. Det drejer sig om

1. C.C. Lous: Styrmands-Kunst eller saa kaldet Skatkammer, Kiøbenhavn 1787. Dett er en lærebog for styrmænd i såvel handelsflåden som orlogsflåden, og den blev brugt på både søfartsskolerne rundt om i riget og på søkadetakademiet i København. C. C. Lous var såkaldt navigationsdirektør.

2. Thomas Bugge: De første Grunde til den sphæriske og theoretiske Astronomie samt den mathematiske Geographie, Kiøbenhavn 1796. Dette er en lærebog beregnet for universitetsstuderende. Thomas Bugge var professor ved Københavns Universitet i matematik og astronomi.

I. LOUS 

Hos Lous s. 287 finder vi en beskrivelse af de to korttyper:

Tekst

Kommentar

 Da vi nu skulle give Regler for Seiladsen paa de store Vande, hvorledes at indrette den efter Landenes Beliggenhed for at naa sit tilagtede Sted, maae vi først betænke, at al Seilads skeer paa Jordens runde og kugelagtige Overflade, hvoraf man til Brug paa Søen ei vel kan giøre en fuldkommen Afbildning; at man derfor maae nøies med at aflægge i Plan det Stykke af Jordens ydre Side, som indtager et vist Farvand. Dog dette haver sin Vanskelighed; thi Meridianerne og Parallelerne som bestemme Brederne og Længderne, saavelsom Compasstregerne, som give Courserne og Distanserne, ere alle krumme Linier, hvilke naar de udstrækkes i Plan, nødvendig komme ud af deres Skik, Sammenhæng og Maal. For at iværksætte det med mindste Feil, betiener man sig af tvende Maader: enten aflægger man et meget lidet Stykke af Jorden, som en Plan, i hvilket Tilfælde Feilene saa godt som forsvinde, da de før meldte krumme Linier paa saa liden en Plet af Jorden eller af Globusen, som forestiller Jorden, blive næsten rette; og denne Aflægning kaldes det platte Kaart; eller man udstrækker Brede-Graderne paa Meridianerne i samme Proportion, som Længde-Graderne, alt som de nærme sig imod Polerne, aftage, hvorved skeer, at Længde-Graderne paa alle Breder blive lige, at Meridianerne blive rette Linier overalt parallele med hinanden, og at Compasstregerne udstrækkes fra spirale til rette Linier. Denne aflægning, som den rigtigste, man endnu har fundet paa til at bringe et temmeligt Stykke af Globusen i Plan, kaldes det voxende Kaart. Hensigten med begge Slags Kaarter er, at man skal kunne finde Coursen og Distansen imellem Stederne. I begge er derfor Compasstregerne bragte til rette Linier, paa det man kan afsætte eller søge sineCourser endog paa Fierdedeel Streger, ja paa Grader. Og for at finde Distanserne, har man altid i det platte Kaart en Mile-Skale, hvilken ikke kan feile meget, naar kuns Kaartet indbefatter ikkun saa liden en Deel af Jordens Yderste, at dens Rundhed deri bliver ukiendelig. I det voxende Kaart tiener en Meridian i Steden for Mile-Skale hvoraf hver Grad regnes for 15 Danske eller Hollandske Mile, 20 Engelske eller Franske etc. efter hvad Mile man bruger, og ved denne afpasses Distanserne paa deres tilhørige Breder.

 

 
 

  

En parallel er her det samme som en breddecirkel.
Compasstregerne… ere .. krumme Linier : Hvis man på en globus begynder et sted og hele tiden følger en kurs f.eks. mod nordøst, vil man bevæge sig på en kurve der i en spiral nærmer sig nordpolen. 
 

Kaart er en anden stavemåde for kort.”Udstrækningen” forklares nærmere senere




 spirale: se ovenfor

  


Compasstregerne .. rette Linier er af afgørende betydning!

Et kompas er inddelt i 32 streger (se bestikregning), så en fjerdedel streg svarer til 360/128 grader = 2 grader og 48 ¾ minut.
1 grad svarer til 15 danske mil, da 1 bueminut = 1 sømil og 4 sømil = 1 dansk mil.

Dette var formentlig nogenlunde forståeligt, selv om sproget lyder lidt underligt, men det jo også skrevet for mere end 200 år siden.

Det bliver vanskeligere, når Lous går videre og i detaljer forklarer hvordan det at  ”man udstrækker Brede-Graderne paa Meridianerne i samme Proportion, som Længde-Graderne” egentlig skal forstås. Han skriver: 

Tekst
 

Kommentar
For at forklare dette noget nøiere, saa lad i hosstaaende Figur (ligesom tilforn i den tredie Figur) PlpL betegne Jordkloden, Ll Linien eller Æqvinoktialen, P Nord- og p Syd-Polen.
Efterdi da alle Meridianer, som pBP, pAP, plP, ere Halvcirkler, som løbe sammen i Polerne, maae man søge et Middel, hvorved disse Meridianer kunne forebildes som rette Linier, og parallel-løbende med hinanden, saasom BP, AC, GD og lE.

 

 Men af denne Figur er det klart, at, naar BA, AG eller Gl tages hver for en Deel af Længden paa Æqvinoktialen, blive disse Dele altid mindre paa andre Paralleler, det er: at IF eller HM er hver mindre end BA, og jo nærmere Polen, jo større er Forskiellen. For da at bringe disse Meridianer til rette Linier maae Breden i det voxende Kaart ligesaa meget voxe eller forøges, som Længden forstørres.

 

  

Linien = Æqvinoktialen = Ækvator 

pBP ses lige forfra og ligner derfor en ret linje, men det er altså en halvcirkel ligesom PAp osv.

 

 


 

Paralleler er stadig breddecirkler (f.eks. NO og QR).

 

 Den sidste sætning her er afgørende: ”maae Breden i det voxende Kaart ligesaa meget voxe eller forøges, som Længden forstørres”. Men det er ikke for at meridianerne skal blive til rette linjer, som Lous skriver, det er for at ”kompasstregerne” skal blive rette linjer! En fast kompaskurs skærer nemlig alle meridianer under en bestemt vinkel, idet enhver meridian jo udpeger retningen nord-syd. Og hvis meridianerne i det ”voksende kort” er parallelle rette (lodrette) linjer, skal en fast kompaskurs også følge en ret linje på kortet for at kunne skære alle meridianerne under samme vinkel. 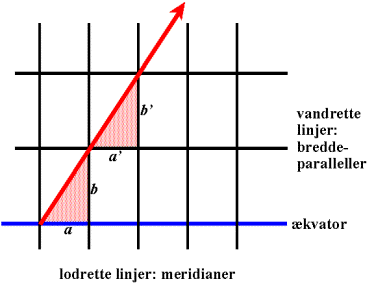Se på følgende figur: 
 

 På figuren er den skrå linje med pil en fast kurs.
Det er her klart, at når både meridianerne og breddeparallellerne afbildes i planen som parallelle rette linjer, så må de to farvede trekanter på figuren være ensvinklede. Derfor må der gælde, at
                                                                                .

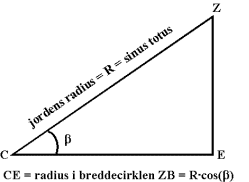
Når nu a og a’ faktisk er afsat som lige store på kortet, men a’ ligger på en breddeparallel højere oppe, så må den virkelige afstand på denne breddeparallel mellem de to viste meridianer være mindre (som Lous forklarede det ovenfor). Med andre ord er a’ tegnet for stor – lad os sige at a’ er k gange så stor som den er i virkeligheden. Da forholdet  er det samme som , må b’ derfor også tegnes k gange så stor.

Det fremgår også af Lous’ forklaring at k bliver større og større jo højere breddeparallellerne ligger.
Spørgsmålet er så: kan vi finde ud af hvad k er?
Det forklarer Lous i det næste afsnit. Det er her vigtigt at vide, at man tidligere betegnede kateterne i en retvinklet trekant som sinus og cosinus, så deres talværdi altså afhang af hvor lang hypotenusen var; i en tabel kunne man f.eks. sætte hypotenusen til 100.000. Vi underforstår i dag  altid at hypotenusen er 1, derfor må vi gange med hypotenusens længde (R) i teksten nedenfor:  

Tekst
 

Kommentar

Siden nu Længde-Forskiellen BA under Linien er paa Parallelen af NO ei større end IF og paa Parallelen QR ei større end HM, saa kiendes deraf, hvad Forholden bliver af Længden imod Breden, nemlig paa Parallelen NO, som den sande Længde IF til udstrakte Længde If, saaledes den sande Brede til den voxende Brede, eller paa parallelen QR som den sande Længde HM til den udstrakte Længde Hm, saaledes den sande Brede til den voxende Brede.

Og efterdi Omkredsen eller en vis Omkredsens Deel af Æqvinoktialen og Stor-Cirklen Ll forholder sig mod Omkredsen eller ligesaa stor Omkredsens Deel af enhver parallel Cirkel som NO, ligesom Radius af Æqvinoktial-Cirklen LB til Radius af Parallel-Cirklen NI, saa følger, at en Længde-Grad under Linien forholder sig til en Længde-Grad under Parallelen NO, som BL lig BN, d.e. Radius til NI, som er Sinus af Vinklen NBI eller Sinus-Complement af Breden NL; og herpaa grunder sig Udregningen af den voxende Brede-Tavle, som igien er Grunden til det voxende Kaarts Aflægning.

Linien = Ækvator

  

 

 
 

Omkredsen af en cirkel er 2π ∙ radius , derfor er forholdet mellem to cirklers omkredse lig med forholdet mellem deres radier: 

 ,

og vinkel NBL er bredden for breddeparallellen NO.

Forholdet mellem omkredsene er lig med forholdet mellem radierne. Men så er forholdet mellem 1/360 af omkredsene også lig med forholdet mellem radierne. Dvs

.

Når de to størrelser er tegnet lige store på kortet, er graden på breddeparallellen altså tegnet  gange for stor – og dermed har vi fundet det k vi søgte!

På den pågældende breddegrad skal afstanden mellem to på hinanden følgende breddegradscirkler (f.eks. med et bueminuts afstand) altså tegnes  gange så stor som ved ækvator.

Derfor ser det på det ”voksende kort” ud som om breddegraderne vokser, jo længere man kommer mod nord. 

Eksempler:
Ved ækvator er afstanden mellem to breddegradscirkler med et bueminuts afstand lig med længden af et bueminut på en storcirkel, dvs en sømil.
Ved 32 graders nordlig bredde er afstanden sømil ≈ 1,18 sømil.
Ved 45 graders nordlig bredde er afstanden sømil ≈  1,41 sømil.
Ved 72 graders nordlig bredde er afstanden  sømil ≈ 3,24 sømil. 

Lous har bag i sin lærebog 12 siders ”Tabel over den voxende Brede i tiende Deel Minutter”. 

 

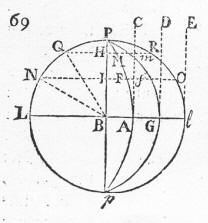
II. BUGGE 

Vi prøver nu at se på beskrivelsen af det samme i Bugges lærebog i astronomi og matematisk geografi. Nærmere bestemt § 14 og !5 i den ”Mathematiske Geographie”. (Se § 14 og 15 her)

Den figur, der henvises til findes på Tavle 11 som fig. 73 og gengives her: 
 

 

Tekst
 

Kommentar

§ 14.

Længde-Cirklen igiennem et givet Sted Z, eller Parallelen igiennem Z, er en liden Cirkel ZB parallel med Æqvator AQ. Naar Jorden er kugelrund, saa maa Graderne af alle Meridianer eller alle Brede-Grader være indbyrdes lige store, og alle lige store med Graden af Æqvator; efterdi alle Kuglens store Cirkler have samme Radius som Kuglen selv.[..] Parallelerne derimod ere smaa Cirkler; deres Flader gaae ei igiennem Kuglens Center, og deres Omkreds og deres Grader blive mindre og mindre, jo meer de nærme sig til Polerne, eller jo større Breden ZQ af Stedet Z er [..].
Graden af Æqvator eller af Meridianen, forholder sig til Graden af Parallelen, som Sinus totus til Cosinus af Breden ZQ.
Kald Graden af Æqvator AQ = G, og af Parallelen ZB = g. Man drager fra Q Linien QC perpendikular til Jordens Axel Pp, saa er CQ Radius til Æqvator; ligeledes drages til Pp Perpendikularen ZD, som bliver Radius til Parallelen ZB; man drager ZE perpendikular til CQ, og Linien CZ = CQ. I den retvinklede Triangel CEZ er CZ = CQ Sinus totus [..], og CE er Cosinus til ZQ [..]; altsaa CZ eller CQ : CE = sin. tot : cos. ZQ, eller Radius af Æqvator : Radius af Parallelen = sin. tot : cos. ZQ; men Cirklers Peripherier forholde sig som deres Radier [..]; altsaa Peripherien af Æqvator : Peripherien af Parallelen = sin. tot : cos. ZQ; naar man nu deler disse Peripherier i 360 lige Parter eller Grader, saa maa Qvotienterne forholde sig som de dividerte Tal (§. 74 Arith.);
 følgeligen

 :  

eller Graden af Æqvator : Graden af Parallelen =
G : g = sin. tot : cos. ZQ.

 

  

 

 

 

 

 

 

 

Perpendikular = vinkelret


Sinus totus  (forkortes sin. tot.)betyder her hypotenusen.
ZQ er det samme som vinkel ZCQ, altså bredden for breddeparallellen BZ.

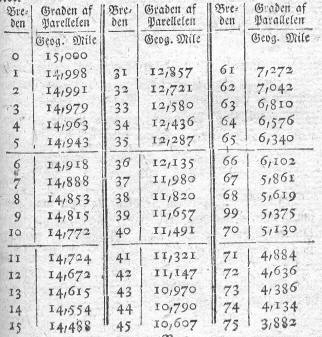
 Derpå følger en forklaring på hvordan man finder afstanden mellem to på hinanden følgende hele længdegrader, når man befinder sig på en bestemt bredde (”Graden af Parallellen”): 

Tekst

Kommentar
 

Graden af Parallelen findes ved at multiplicere Graden af Æqvator med Cosinus af Breden; thi G : g = sin. tot : cos. ZQ; men sin. tot. = 1; altsaa G : g = 1 : cos. ZQ; og G x cos. ZQ = g.

Eksempel.  Graden af Æqvator eller Meridianen = 15 geographiske Mile; man spørger om Graden af Parallelen eller Længde-Cirkelen igiennem Kiøbenhavn, hvis Brede er = 55º 41´.
Graden af Æqvator = G = 15 Mile.
                      cos. 55º 41´ = 0,564
                      ________________
                                                  60
                                                90
                                              75
                      ________________
                               g = 8,460 Mile. 

Graden af Parallelen igiennem Kiøbenhavn er paa det allernærmeste 8½ geographiske Mile.
 

 Her regnes der med at hypotenusen = sinus totus er 1
 

Geografisk mil = dansk mil (= 4 sømil)

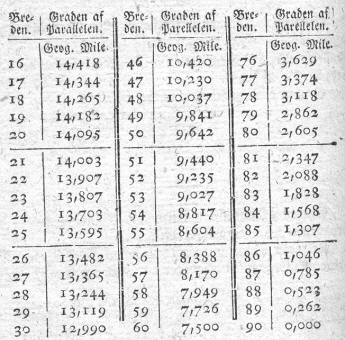
 Bugge udregner derpå en tabel for længden af en grad på alle breddecirkler med hele breddegrader: 

 

Følgende Tavle viser Størrelsen af Parallelen, udi geographiske Mile; fra Æqvator til Polen for hver Grad af Brede.
 

[se § 14 og 15 her]

Bugge kommer altså ikke ind på konstruktionen af ”det voksende kort”.