Breddebestemmelse for lejr II 17. april 1912

Download dette dokument i Word-format
Download dette dokument i pdf-format

Vi vil her detaljeret gennemgå processen fra observationer til udregning af bredde.
En beskrivelse af den anvendte teodolit kan ses her og en redegørelse for anvendelsen til zenitdistanceobservationer kan ses her.

Dette er en observationstabel for 17. april 1912 i Peter Freuchens dagbog.

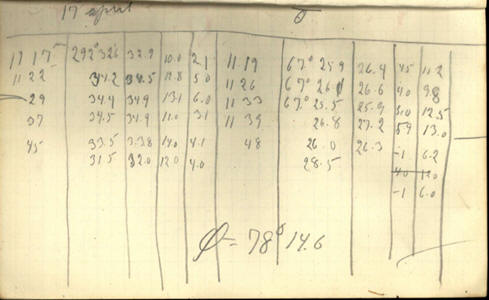
Ved renskrivningen kommer skemaet til at se sådan ud:

Peter Freuchens brug af decimaladskiller er svingende i dagbogen. Somme tider bruger han det engelsk/amerikanske decimalpunktum (som her), somme tider bruger han det dansk/tyske decimalkomma (som f.eks. i skemaet til lejr VIII 24. april). Det må man bare vænne sig til.

Vi skal bruge zenitdistancen (vinklen mellem sigtelinjen til solen og sigtelinjen til zenit) til at finde bredden. Derfor skal vi kun måle lodrette vinkler, så vi får ikke brug for aflæsning på den vandrette skala på teodolitten.

Symbolet Ō  betyder at der er målt fra solens øvre kant. Da vi skal bruge solens centrums zenitdistance, skal vi lægge solens halve diameter til til sidst; den er ifølge Nautisk Almanak 1912 16’.

Skemaet har 10 kolonner. Kolonne nr 1 og kolonne nr 6 fra venstre angiver de klokkeslet, hvor observationerne foretages.

Kikkert til venstre (Steno Museet)	Kikkert til højre (Steno Museet)

Først stilles teodolit og kikkert helt vandret ved hjælp af nivelleringsskruerne og ved at se på libellerne.
Dernæst sigtes mod solens overrand med kikkerten stillet til venstre; her aflæses kl 11 17 vinklen v = 292°32’.6 på nonius A (kolonne 2). På nonius B aflæses minutterne til 32’.9 (kolonne 3).  Zenitdistancen er så 360° – v, hvor v ligger mellem 292°32’.6 og 292°32’.9.
Så drejes teodolitten 180° om sin lodrette akse, så kikkerten er stillet til højre. Kikkerten drejes om sin vandrette akse så den igen sigter mod solens overrand, denne gang med kikkerten stillet til højre. Her aflæses så kl 11 19 vinklen z = 67°25’.9 på nonius A (kolonne 7). På nonius B aflæses minutterne til 26’.4. Zenitdistancen er så z, hvor z ligger mellem 67°25’.9 og 67°26’.4.
Tiendedelene af minutter fremkommer ved et skøn ved aflæsningen – man kan jo kun aflæse præcist ned til halve minutters nøjagtighed.

Men hvad med kolonnerne 4, 5, 9 og 10? Det er aflæsninger af de to libeller. Disse aflæsninger kan bruges til yderligere korrektion ved beregning af bredden. Dette er demonstreret detaljeret i dokumentet Hildebrand_libelleskalaer, men her vil vi ikke komme nærmere ind på det, så i det følgende registrerer vi blot at kolonnerne eksisterer, men ignorerer dem ellers (se dog opgaven til slut, der ansporer til at regne korrektionen ud).

Tabellen kan nu se sådan ud forsynet med overskrifter over hver kolonne. vA og vB er værdier af 360° - zenitdistancen målt på henholdsvis nonius A og nonius B med kikkerten til venstre, mens hA og hB  er værdier af zenitdistancen målt på henholdsvis nonius A og nonius B med kikkerten til højre.

For at gøre det mere gennemskueligt tilføjer vi to kolonner (grå baggrund), hvor vi udregner zenitdistancen med kikkerten stillet til venstre:

Kikkert til venstre							Kikkert til højre
Klokke-slet	vA	vB	360° - vA	360°-vB	Lib 1	Lib 2	Klokke-slet	hA	hB	Lib 2	Lib 1
11 17 m	292°32’6	32.9	67°27.4	27.1	10.0	2.1	11 19	67°25.9	26.4	4.5	11.2
11 22 m	34.2	34.5	67°25.8	25.5	12.8	5.0	11 26	67°26.0	26.6	4.0	9.8
29	34.4	34.9	25.6	25.1	13.1	6.0	11 33	67°25.5	25.9	5.0	12.5
37	34.5	34.9	25.5	25.1	11.0	3.1	11 39	26.8	27.2	5.9	13.0
45	33.5	33.8	26.5	26.2	14.0	4.1	48	26.0	26.3	-1	6.2
	31.5	32.0	28.5	28.0	12.0	4.0		28.5		4-0	12.0
										-1	6.0

Hvis vi til slut stiller resultaterne for zenitdistancemålingerne op i et skema får vi:

Vi kan her se, at  67°25’.3 er den mindste middelzenitdistance, der er målt, svarende til den største solhøjde 22°34’.7.

Solens deklination den pågældende dag har Peter Freuchen slået op i en medbragt deklinationstabel, det kunne være Nautisk Almanak 1912.

Vi skal have en cirkaværdi for tidsafstanden til Greenwich. Da lejr II ikke er så langt inde og udgangspunktet Thule har en længde på ca 68° vest (også ifølge Peary-kortet), og 15° i længdeforskel svarer til en times tidsforskel (hvorfor det?), kan vi regne med at tidsafstanden til Greenwich er ca 4½ time, dvs solen kulminerer på denne position 4½ time senere end ved Greenwich.
For at gøre livet lettere benytter vi internettet i stedet for Nautisk Almanak til at finde deklinationen. På The Online Nautical Almanac kan vi nederst på siden indtaste datoen 04/17/1912 og derpå  gå ned til ”SUN” og 17. april og aflæse ud for kl 16.30 (4½ time efter kl 12) deklinationen 10°30’.8.

Refraktionen kan findes ved hjælp af den tabel som J. P. Koch anfører.
Det fremgår af Peter Freuchens dagbog, at temperaturen er -27.3 grader og barometerstanden er 644 mmHg. Ifølge tabellen finder man så refraktionen som 2’.35 gange 1.16 gange 0.85 = 2’.3.

Vi kan nu beregne bredden b som:

b = zenitdistance + solens halve diameter + deklination + refraktion = 67°25’.3 + 16’ + 10° 30’.8 + 2’3 = 78°14’.4.

Som det ses, har Peter Freuchen beregnet bredden til φ = 78°14’.6, hvilket jo er meget tæt på. Forskellen kan muligvis skyldes en anden måde at finde refraktionen på. Men det kan også skyldes, at Peter Freuchen faktisk har taget hensyn til den korrektion, der kan beregnes ud fra libelletallene.

OPGAVE:
Bestem hvor stor en korrektion libelletallene giver anledning til, hvis hver streg på libellen svarer til 20’’.5. Se hvorledes beregningen udføres her. Tag kun de første fem målinger med.