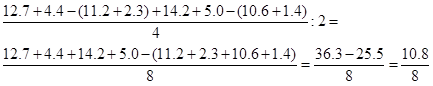|
|
|
geomat.dk : Opdagelser & navigation : Instrumenter : Hildebrands lille rejse-teodolit - anvendelse af libelleskalaerne |
|
Hildebrands lille
rejse-teodolit - anvendelse af
libelleskalaerne Download dette
dokument i Word-format Følgende beskrivelse af,
hvordan libelleskalaerne har været anvendt,
støtter sig på J.P. Koch:
Survey of Northeast Greenland.
Meddelelser om Grønland XLVI, 1917.
J.P. Koch skriver p.204:
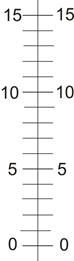
The
divisions on the level of the vertical
circle were nearly 20’’, on the level of the
axis nearly 30’’. Vi vil her kun
interessere os for libellen for den lodrette
kreds, da det er den der benyttes I
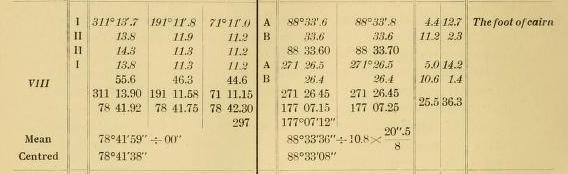
forbindelse med måling af zenitdistancer. Den første kilde er en
tabel på p.206 og 207, hvor Koch angiver
målinger af horisontale vinkler fra station
V på Lille Koldewey til forskellige andre
stationer. Disse målinger ledsages desuden
af målinger af de pågældende stationers
zenitdistancer, set fra station V.
Det er målinger til højre
for den kraftige lodrette linje, der angiver
zenitdistancerne. Der måles i to omgange:
levelling 1 og levelling 2.
Koch skriver på p. 205:
Attention is drawn to the fact that the four
upper readings of the level correspond to
the first leveling, the four lower ones to
the second leveling. Det er
derfor vi ved at libelletallene hører sammen
med målingerne som vist i ovenstående tabel.
Vi ser først på
levelling 1:
Det formodet vandrette
niveau er derfor for højt i objektivsiden,
og zenitdistancen derfor for stor.
Aflæsningen af zenitdistancen skal derfor
formindskes med 0.9 libellestreger; idet
Koch regner med 20’’.5 for hver
libellestreg, betyder det en formindskelse
med 18’’.5. Så ser vi på
levelling
2:
Det formodet vandrette
niveau er derfor for højt i objektivsiden,
og zenitdistancen derfor for stor.
Aflæsningen af zenitdistancen skal derfor
formindskes med 1.8 libellestreger; idet
Koch regner med 20’’.5 for hver
libellestreg, betyder det en formindskelse
med 36’’.9. Hvis vi kigger på de to
levellings under ét, giver de altså
anledning til en gennemsnitlig formindskelse
af zenitdistancen på (18’’.5 + 36’’.9)/2 =
27’’.7. Hvis vi afrunder til 28’’ er det
præcis hvad Koch regner ud i tabellen:
Hvorfor er det nu det
samme? Jo, for vi har udregnet for levelling
1:
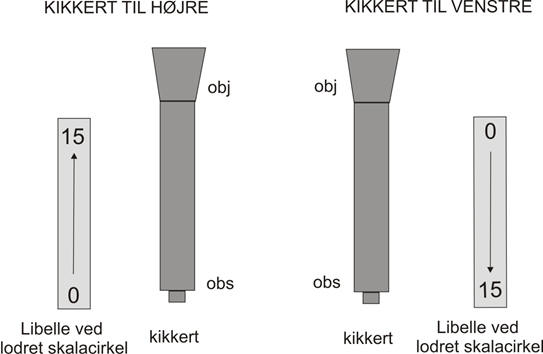
36.3 er summen af libelletallene for kikkert til højre og 25.5 er summen af libelletallene for kikkert til venstre. Hvis differensen mellem disse to summer er positiv, må den gennemsnitlige forskydning, når vi går fra kikkert til højre til kikkert til venstre gå i retning væk fra objektivet (se figur nedenfor). Og hvis boblemidten forskyder sig væk fra objektivet, må det betyde at kikkerten sigter for lavt. Så bliver den målte zenitdistance for stor, og vi må trække libellekorrektionen fra. Og det er netop hvad Koch gør i det viste eksempel. Tilsvarende gælder, at
hvis differensen er negativ, skal vi lægge
libellekorrektionen til.
Man kan vise, at dette kan
udvides til en generel regel:
OPGAVE: [De viste foto er alle af
Hildebrand-teodolitten på Steno Museet]
|


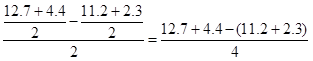 som boblemidtens
forskydning fra hvor den burde være.
som boblemidtens
forskydning fra hvor den burde være.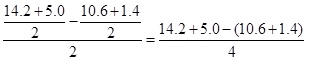 som boblemidtens
forskydning fra hvor den burde være.
som boblemidtens
forskydning fra hvor den burde være.