For at finde længdeforskellen mellem to steder skal man først finde den nøjagtige tidsforskel mellem dem. Tid er imidlertid ikke bare tid. Der er flere former for tidsmåling:

Sand tid

Når solens midtpunkt passerer en observatørs meridian siges tiden at være "sand middag." P.g.a. jordens omløb omkring solen er tiden mellem "sand middag" og næste dags "sand middag" IKKE konstant. Hvis man skulle basere tidsregning på "sand tid" ville dagene derfor ikke blive lige lange. "Sand tid" egner sig derfor i praksis ikke til tidsangivelse.

Middeltid

Mangelen på regelmæssighed i "sand tid" undgåes i det såkaldte "middelklokkeslæt", som derfor kan bruges til praktisk tidsregning. Som grundlag for "middelklokkeslættet" forestiller man sig et punkt (kaldet "middelsolen"), som i modsætning til den sande sol set fra jorden løber jævnt over himlen. Udgangspunktet for "middelsolen" er valgt, så forskellen mellem den og den sande sol er mindst mulig. Efter 1 år mødes "middelsolen" og den sande sol i udgangspunktet, men i mellemtiden er "middelsolen" løbet i en fuldstændig regelmæssig bevægelse over himlen.
Når "middelsolen" står i meridianen kaldes tidspunktet "middelmiddag". Fra en "middelmiddag" til den næste er der 24 "middeltimer" - de timer vi til dagligt bruger til at inddele dagen med. Med mindre andet er bemærket menes middeltid med enhver tidsangivelse.

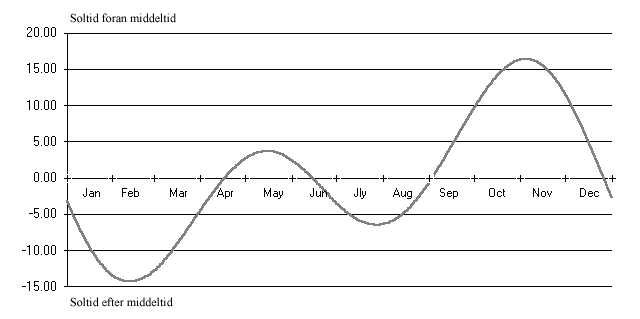
Middeltiden er udgangspunktet for den tidsregning vi bruger i dag. Middeltiden på 0-meridianen i Greenwich (Greenwich Mean Time = GMT = Greenwich Middel Tid) bruges som udgangspunkt for tidregning overalt på jorden.

Zonetid

Da man ikke kan bruge den samme tid overalt på jorden er den inddelt i tidszoner á 15°. Danmark ligger i zonen GMT + 1, d.v.s den tid vi bruger er Greenwichs middeltid + 1 time. Da 1 times tidsforskel svarer til 15° er GMT + 1 middeltiden på meridianen 15°Ø - d.v.s.en meridian der går gennem Sverige. Grænsen mellem zonerne går midt imellem meridianerne 15°Ø, 30°Ø o.s.v... l. F.eks. går grænsen mellem GMT og vores GMT + 1 på 7½°Ø.

Tidsekvationen

Tidsekvationen betegner afvigelsen mellem middeltid og sand tid. Tidsekvationen varierer over året, fra ca. -15 min. til ca. +17 min. Tidsekvationen Tj beregnes af følgende udtryk:

hvor B indsættes i grader og beregnes af: 

hvor n er dagens nummer (ud af 365 eller 366 ved skudår).

Ligning og figur er fundet på www.formel.dk og bearbejdet.

Øvelse
Forklar kort hvad de forskellige tider betyder. Hvis vi ser på tidspunktet kl 12 i zonetid (d.v.s. den tid vi alle går rundt og bruger til daglig) d. 1/10 i København (som ligger på ca. 12°34' øst for Greenwich), hvad er så GMT? Og middeltid og sand tid for København? (man behøver ikke regne den korrekte tidsekvation ud for at løse opgaven - bare aflæs en cirka-værdi på grafen). Se evt. afsnittet om Længdegrader og tid.