Daviskvadrant
- instrumentbeskrivelse og virkemåde
Download
dette dokument i
Word-format.
Download
dette dokument i
pdf-format.
|
Geomat har to
lidt forskellige daviskvadranter til
udlån.
Den ene daviskvadrant er bygget af
Søren Mølstrøm i Århus efter målene
på en original daviskvadrant, der
befinder sig på Åbenrå Museum. Der
er foretaget visse forenklinger,
således er der på kopien ikke nogen
transversalskala på den store bue.
Den anden daviskvadrant er bygget af
Gregg Germain i USA
http://home.comcast.net/~saville/back_staff.htm
). Den er forsynet med
transversalskala på den store bue,
men til gengæld angiver skalaen på
den lille bue kun hver femte grad.
Daviskvadranten
er et navigationsinstrument, der
havde sin storhedstid i
16–1700-tallet (se daviskvadranten,
historie). Instrumentet brugtes
udelukkende til måling af
solhøjden (eller dennes
komplementvinkel, solens
zenitdistance). På engelsk
kaldtes instrumentet også
backstaff, fordi man målte
solhøjden med ryggen til solen, i
modsætning til når man skulle måle
med jakobsstaven (som derfor også
kaldtes fore-staff). |
Udseende
 |
| Figur 1.
Daviskvadranten transporteres i en
stor, flad kasse. Her ses, hvorledes
instrumentets dele er anbragt i
kassen. |
 |
| Figur 2.
Daviskvadranten samlet med de tre
kryds anbragt på plads. |
|
Til brug for
målingen er instrumentet forsynet
med tre tværgående stykker træ,
såkaldte kryds.
Disse kryds benævnes
horisontkrydset,
skyggekrydset og sigtekrydset,
og de anbringes på instrumentet som
vist på fig. 2.
Krydsenes udseende er vist i
nærbilleder nedenunder: |
|

Figur 3.
Horisontkrydset og skyggekrydset.
|

Figur 4.
Sigtekrydset.
|
| Det ses, at
horisontkrydset er forsynet med en smal
vandret sprække. Sigtekrydset er forsynet
med et lille hul, hvorigennem man sigter hen
på sprækken i horisontkrydset. |
Opbygning
Daviskvadranten er
opbygget af to buestykker. Det ene har en
lille radius og spænder over 65 grader, det
andet har en stor radius og spænder over 25
grader. Tilsammen spænder de to buer over 90
grader, og det er derfor instrumentet kaldes
en kvadrant.
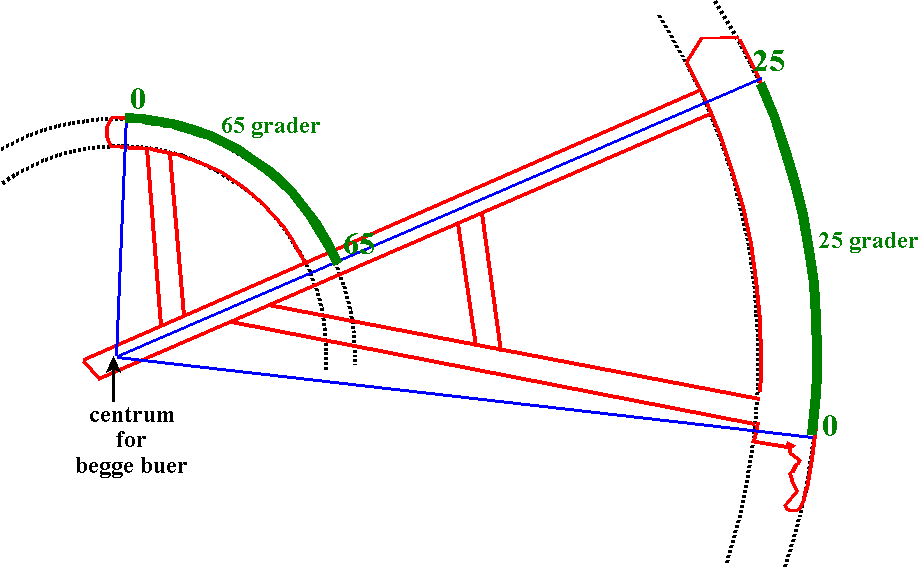
Den geometriske opbygning kan ses på
følgende figur: |
 |
|
Figur 5.
[Forstørrelse ved klik på billede]
|
Hvordan udføres en måling?
Man måler altid to
vinkler på instrumentet, én på den lille
bue og én på den store.
|

Figur 6.
Måling af solhøjden – således holdes
instrumentet
|
|

Figur 7.
Skyggekrydsets skygge på
horisontkrydset.
|

Figur 8.
Skyggekrydset anbragt på den lille
bue og sigtekrydset på den store
bue.
|
|
1)
Skyggekrydset anbringes i en
passende position på et helt antal grader på
den lille bue. Det angivne gradtal skal være
under det antal grader man skønner
zenitdistancen til.
2)
Gennem sigtekrydsets lille hul
sigter man på sprækken i horisontkrydset og
drejer instrumentet sådan, at man tillige
kan se horisonten gennem sprækken.
3)
Nu varierer man sigtekrydsets
position på den store bue indtil man gennem
hullet i sigtekrydset kan se skyggekrydsets
skygge på horisontkrydset, sådan at den
øverste del af skyggen flugter med
horisonten set gennem sprækken.
4)
Til sidst aflæser man de to
vinkler a og b på henholdsvis den lille bue
og den store bue – se fig.9 og 10.
|
|
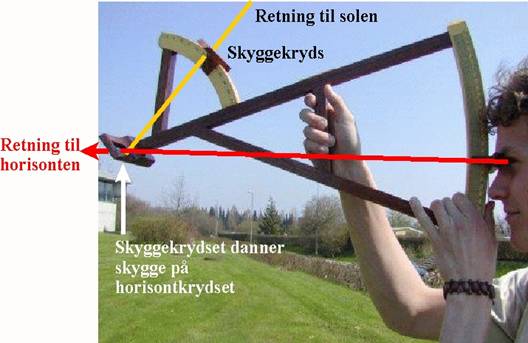 Figur
9. Figur
9.
|
|
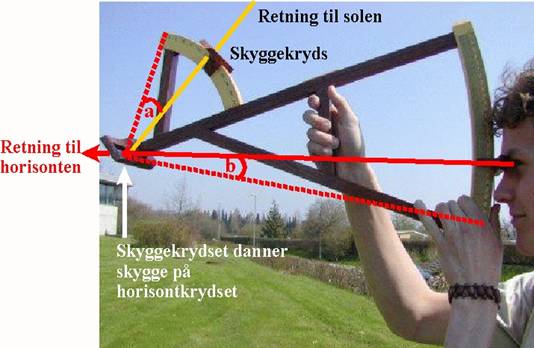 Figur
10. Figur
10.
|
Hvordan aflæser man
de to vinkler?
|

Figur 11.
Aflæsning på lille bue.
|

Figur 12.
Aflæsning på store bue.
|
|
Aflæsning på den lille
bue (se fig.11): Skyggekrydsets øverste kant
står ved 39 grader på den lille bue. Man
aflæser altså 39 grader.
Aflæsning på store bue (se fig.12):
Sigtekrydsets hul ligger i krydsets
vandrette midterlinje. Denne midterlinjes
beliggenhed er markeret med det stykke af
krydset, der går ind over den store bue.
Positionen aflæses til 11 grader og 40
bueminutter.
De to aflæste gradtal lægges sammen og man
får dermed solens zenitdistance, som
altså i dette tilfælde er 50 grader og 40
bueminutter.
På daviskvadranten
bygget i USA foretages aflæsningen som vist
på følgende figurer: |
|

Figur
13.
Aflæsning på lille bue.
|

Figur
14.
Aflæsning på stor bue.
|
|
I princippet kan man
ved hjælp af transversalskalaen på den store
bue aflæse vinkler med en nøjagtighed på 1 bueminut. I praksis er det næppe realistisk
at regne med mindre end spring på 10
bueminutter.
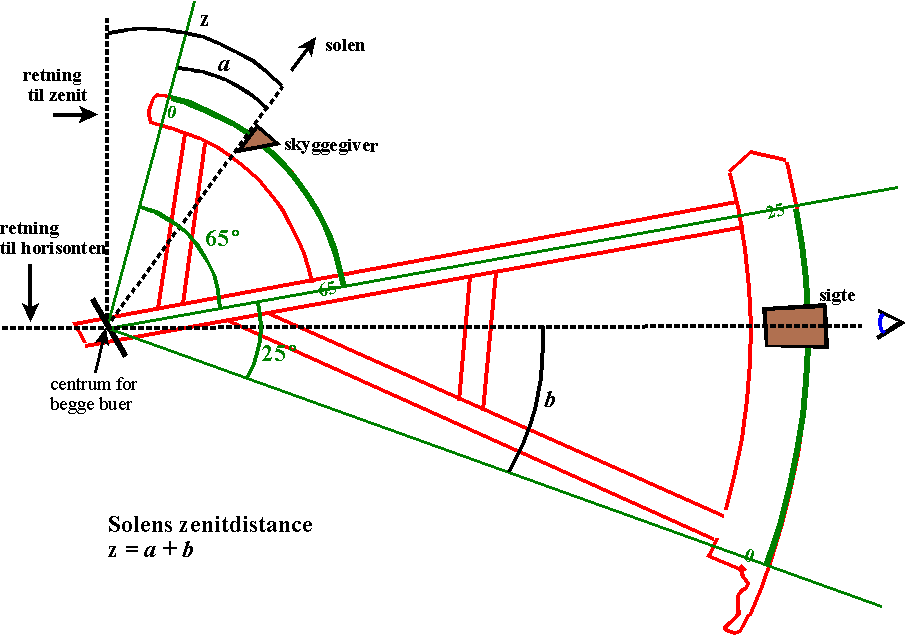
At summen af de to
aflæste gradtal faktisk giver zenitdistancen
kan man se på den næste figur:
|
 |
|
Figur 15.
[Forstørrelse ved klik på billede]
|
Opdateret 6. september 2009
|














