Thomas Bugge: De første Grunde til den rene eller abstrakte Mathematik. Tredje og sidste Deel. Den oekonomiske og den militaire Landmaaling. Kiøbenhavn 1814.
Download dette dokument i Word-format.

Download dette dokument i pdf-format.

 Femte Kapitel.

Utilgiengelige Liniers Opmaaling.

Ved den allermindste Øvelse i Marken vil man strax erfare, at ei alle Linier og ei alle Distancer med Kieden virkeligen kan opmaales formedelst forekommende Hindringer af Moser, Søer, Skove, Byer o.s.v. Saadanne Linier, hvilke med Kieden ei virkeligen kan maales, kaldes utilgiengelige Linier eller Distancer. Det er højst fornødent, at forklare de geometriske Haandgreb og den Anvendelse af Maalebordet, hvorved saadanne Linier med samme Nøiagtighed kan bestemmes, som om de med Kieden vare opmaalte. Disse Problemer ere saa meget vigtigere, som de ere Grundvolden til al Landmaaling, og de siden skal anvendes til Opmaalingernes betydelige Forkortning, endog paa de Steder og ved de Linier, hvor Beliggenheden tillod at maale med Kieden.

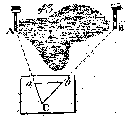
    At Maale en utilgiengelig Linie AB under den Betingelse, at man paa Marken kan finde et Punkt C, hvorfra kan sigtes og maales til A og til B.
    1. Udi Punktet C opstilles Maalebordet horizontalt (§.43).Ved Punktet C paa Bordet, hvilket er bragt lodret over Punktet paa Marken ved Gaffelen (§.44.Num.8), lægges Diopter-Linealens Kant, og Diopter-Linealen, bestandigen liggende ved Punktet C, vrides saalænge, indtil Objektet A er dækket af Sigte-Pladen og staaer midt i Sprækken (§.48), og man opdrager paa Bordet med Passerspidsen Linien Ca, og efter denne Linie udsættes Afstiknings-Stokke paa Marken (§.53).
    2. Derefter sigtes til Objektet B, Linien Cb opdrages paa Bordet, og udstikkes paa Marken.
    3. Naar Bordet er borttagen, fuldføres Afstikningen af Linien AC efter de fra Bordet udsatte Stokke (§.5-9), og denne Linie AC opmaales med Kieden (§.16-19), og findes f.Ex. 500 Alen ¹⁾ .
    4. Ligeledes afstikkes og opmaales Linien CB, og findes f.Ex. 600 Alen.
    5. Efter den Maalestok, i hvilken Opmaalingerne og Kartet skal tegnes, afsættes paa Maalebordet Ca = 500 Alen og Cb = 600 Alen.
    6. Man drager Linien ab, saa indeholder denne efter Kartets Maalestok lige saa mange Alen, som AB indeholder virkelige Alen paa Marken: thi i ) ABC og ) abC er Vinkelen C tilfælleds og de Sider, som slutte denne Vinkel, ere efter Konstruktionen proportionale; altsaa ere Trianglerne ligedanne ²⁾, og Ca : ab = CA : AB (§.152 Geom. ³⁾)

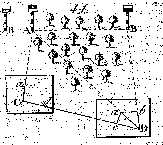
    Dersom man paa Marken ei kan finde et saadant Stations-Punkt, fra hvilket til begge objekter A og B kan sigtes og maales, saa kan den utilgiengelige Linie AB opmaales, naar paa Marken kan afstikkes og opmaales en Grundlinie CD, fra hvis ene Ende-Punkt C kan sigtes og maales ikkun til A, og fra det andet Ende-Punkt D kan sigtes og maales ikkun til B.
    1. Efterat Begyndelsen af Grundlinien CD er afstukken, stilles Maalebordet efter Stokke paa begge Sider og efter Punktet C (§.48), man tager Sigtet til Objektet A (§.48), og opdrager Linien Ca paa Bordet.
    2. Den Sigtelinie Ca udstikkes fra Bordet til Marken (§.53). Bordet nedtages, og man afstikker (§.5) og opmaaler Linien AC paa Marken; og afsætter efter Karters Maalestok Ca paa Bordet, og derved er Stedet a af Objektet A bestemt paa Kartebladet.
    3. Nu fortfarer man med Afstikningen og Opmaalingen af Grundlinien CD, indtil man kommer til Punktet D, hvorfra der kan sigtes og maales til det andet Objekt B.
    4. Grundlinien CD afsættes efter Maalestokken paa Bordet fra c til D; dette Punkt paa Bordet stilles over det Punkt paa Marken, hvor Maalet ophørte, og Grundlinien cD paa Bordet efter Grundlinien CD paa Marken (§.44). Man tager Sigtet til det andet Objekt B og opdrager Sigtelinien Db paa Bordet.
    5. Denne Linie udstikkes paa Marken efter DB, og opmaales. Naar man da afsætter Maalet af DB, saa har man bestemt B paa Marken at ligge i b paa Bordet.
    6. Naar man nu paa Bordet eller Kartebladet drager ab, saa er den efter Kartets Maalestok proportioneret med AB paa Marken; thi man drager Diagonalen AD; saa ere i ) ACD og ) acD Vinkelen C = c, og AC : CD = ac : cD efter Konstruktionen, altsaa ere disse Triangler ligedanne (§.152 Geom. ³⁾) A = a; og D = D, eller DaA udgiør en ret Linie, og CD : cD = AD : aD; men efter Konstruktionen og (§.152 Geom. ³⁾) CD :cD = DB : Db; altsaa AD : aD = DB : Db (§.77 Arith.⁴⁾); og Vinkelen ADB = aDb; følgelig er ) ADB ligedannet med ) aDb; og altsaa DB : Db = AB : ab (§.152 Geom.³⁾)

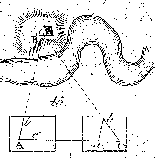
    At opmaale en utilgiengelig Linie AB under den Betingelse, at den ene Ende B er utilgiengelig, men i det andet Punkt A kan tages en Station, og derfra maales en Grundlinie AC, hvor man anden Gang i C kan sigte til B.
    1. Udstikningen af den udseete Grundlinie AC begyndes, og i første Station A opstilles Maalebordet (§.44); man tager sigte til Objektet B (§.48), og opdrager Linien Ab paa Bordet.
    2. Man borttager Maalebordet, afstikker og opmaaler Grundlinien AC (§.5 og 18) indtil Punktet C, hvorfra man kan sigte til B, og Grundlinien afsættes efter Kartets Maalestok fra a til C, hvilket er den anden Station paa Bordet.
    3. Efterat Punktet C paa Bordet er stillet over det modstaaende Punkt paa Marken, og Grundlinien Ca paa Bordet efter Grundlinien CA paa Marken (§.44), tages Sigtet til Objektet B og Linien Cb drages.
    4. Det Punkt b paa Bordet, hvor Sigtelinien fra første Station ab skiærer Sigtelinien fra anden Station Cb, er Stedet af Objektet B; thi i Trianglerne ABC og abC er Vinkelen A = a og C = C; altsaa ere Trianglerne ligedanne (§.149 Num.1 ⁵⁾), og AC : AB = aC : ab (§.148 Geom.⁶⁾), og ved at alternere AC : aC = AB : ab; efter saa mange Alen som AB indeholder paa Marken, saa mange Alen har og ab efter den mindre Maalestok.

___________________________________________________________________________