Månedistancemetoden

Download dette dokument i Word-format
Download dette dokument i pdf-format

Forhistorie

Ret tidligt under de store opdagelser fandt man ud af astronomiske metoder til at bestemme den omtrentlige breddegrad man befandt sig på. Til at begynde med bestod det formentlig blot i at holde øje med hvor højt Nordstjernen stod over horisonten, eventuelt ved at måle med fingerbredder på en udstrakt hånd. Der gik ikke så lang tid, før man også udviklede metoder til at bestemme breddegraden ved hjælp af Solens højde ved middagstid, man har skriftlige vidnesbyrd herom fra første fjerdedel af 1500-tallet.
For at få et kvantitativt mål og ikke bare et kvalitativt, måtte man have instrumenter til at måle højden over horisonten af Nordstjernen og Solen. Hertil benyttede man søastrolabium og kvadrant, og snart kom også jakobsstaven til.

Sagen stillede sig imidlertid helt anderledes, når man skulle bestemme den omtrentlige længdegrad man befandt sig på. I 1530 foreslog Gemma Frisius (1508 – 1555) at bruge et ur til at bestemme længdegraden med, og allerede i 1514 beskrev Johann Werner (1468 -1522) en metode, der gik ud på at måle vinkelafstanden mellem Månen og en stjerne og sammenligne den med samme afstand set fra et andet sted på jorden – den metode, der skulle få navnet månedistancemetoden.
Ingen af de to metoder var imidlertid praktisk brugbare på det tidspunkt; urmetoden (eller kronometermetoden) fordi den krævede ure der gik langt præcisere end nogen ure man kunne konstruere dengang, månedistancemetoden fordi den krævede en præcision i tabellægningen af månens bevægelse som også langt overgik noget man kunne klare i 1500-tallet.

Derfor måtte man nøjes med slutte sig til længdegraden ved en mere indirekte metode, bestikregning. Og der skulle gå hen ved to århundreder, før man var i stand til at benytte de to ovenfor nævnte metoder i praksis. Det skete i anden halvdel af 1700-tallet, og det skete omtrent samtidigt, således at de to metoder kom til at konkurrere i en længere periode.
Her koncentrerer vi os så om den ene metode, månedistancemetoden.

Figur 1. Illustration af månedistancemetoden. 1564-udgaven af Petrus Apianus: Cosmographia, første gang udgivet i 1524.

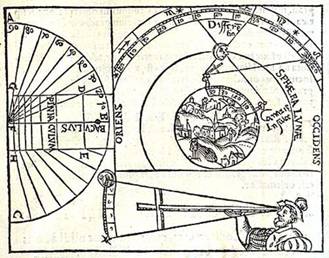
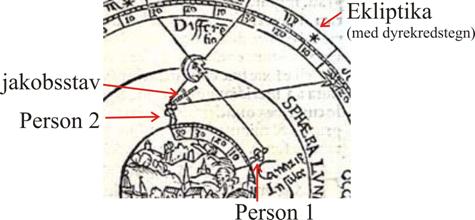
Figur 1 viser brug og konstruktion af jakobsstaven, men det er den øverste figur til højre, der illustrerer månedistancemetoden.

Figur 2. Detalje af  Figur 1, som viser to personer stående på Jordens overflade, den ene udstyret med en jakobsstav.  Cirkelbuen foroven er en del af ekliptika, hvor nogle af symbolerne for dyrekredstegnene er vist tillige med de 30 grader de hver i sær dækker.

Figur 3. Den røde bue på ekliptika er vinkelafstanden mellem Månen og stjernen målt af person 1, og den blå bue på ekliptika er vinkelafstanden mellem Månen og stjernen målt af person 2 (åbenbart med en jakobsstav).  Forskellen mellem disse to buer (benævnt Differentia på figuren) er så et mål for hvor langt de to personer er fra hinanden.

Det fremgår ikke af den viste tegning, hvordan sammenhængen så er mellem den målte vinkelforskel og forskellen i længdegrad mellem de to personer.

Var det vigtigt at kunne bestemme længdegraden?

Svaret er ja, det var overordentlig vigtigt. Først og fremmest var det vigtigt at kunne finde længdegraden til søs af hensyn til skibsfarten, både den militære og den civile. At spørgsmålet havde højeste prioritet kan bl. a. ses af, at både Frankrig og England lod opføre astronomiske observatorier i henholdsvis Paris (1671) og Greenwich (1675), ikke for at drive grundforskning i interessante astronomiske problemer, men udtrykkelig med henblik på ved astronomiens hjælp at blive i stand til at bestemme længdegraden til søs.
Vigtigheden understreges for alvor i 1714, da det britiske parlament udsteder en lov, The Longitude Act, der udlover en dusør på
1) £ 10.000 for en metode til bestemmelse af længdegraden til søs inden for en margen på 60 sømil (111 km),
2) £ 15.000 for en metode til bestemmelse af længdegraden til søs inden for en margen på 40 sømil (74 km),
3) £ 20.000 for en metode til bestemmelse af længdegraden til søs inden for en margen på 30 sømil (55 km).

Princippet i månedistancemetoden

Hvis man måler det nøjagtige klokkeslæt på det sted hvor man er og samtidig konstaterer hvad klokken er i f.eks. Greenwich, kan man beregne tidsforskellen mellem ens geografiske position og Greenwich. Da Solen bevæger sig 360 grader rundt om Jorden på 24 timer (eller rettere, da jorden roterer en hel omgang om sin egen akse på 24 timer), vil tidsforskellen også kunne give længdeforskellen i grader.

Opgave.
Hvis man befinder sig på positionen A klokken 13 lokal tid og finder frem til at klokken i Greenwich samtidig er 9 Greenwich tid, hvilken længdegrad har A så? Greenwich ligger som bekendt på længden 0.

For at kunne finde længdeforskellen skal man altså løse to problemer:

1)      Finde den lokale tid.

2)      Bestemme hvad klokken er i Greenwich samtidig.

Det første problem kunne man f.eks. løse ved at bestemme solens højde ved middag og sætte et medbragt ur efter dette. Det behøvede kun at gå så nøjagtigt at det passede indtil dagen efter, hvor man igen kunne bestemme solens højde – eller næste gang man kunne det.

Det andet problem krævede et medbragt ur, der viste hvad klokken var i Greenwich.
Det problem havde man principielt to måder at løse på. Den ene var at medbringe et mekanisk ur, der gik så godt at det viste Greenwich tid med en tilstrækkelig nøjagtighed under hele sørejsen. Den anden var at betragte Månen som viser på et astronomisk ur, så man ved at se på denne visers position og slå op i en tabel over klokkeslettet i Greenwich for de forskellige positioner af ”måneviseren” også kunne bestemme hvad klokken var samtidig i Greenwich.

Den første metode benævnes kronometermetoden, den anden kaldes månedistancemetoden.

Hvor skaffer man sig så sådan en tabel fra? Det er et helt andet problem. Jorden bevæger sig rundt om Solen i løbet af et år, så set fra jorden flytter Solen rundt mellem stjernerne. Den bane Solen følger på himmelkuglen i sin årlige bevægelse kaldes for ekliptika. Samtidig bevæger Månen sig rundt om jorden på lidt under en måned (27,3 døgn), så Månen flytter sig også i forhold til såvel stjernerne som Solen. Disse bevægelser foregår på så kompliceret en måde, at det i flere århundreder var en fuldkommen uoverskuelig opgave at udarbejde en forudsigelse af Månens, Solens og stjernernes indbyrdes placering i tabelform med spring på kun tre timer.

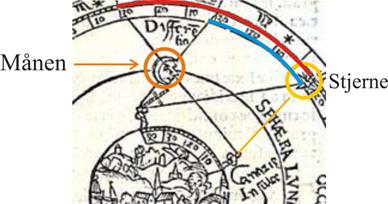
Endelig i midten af 1700-tallet så det ud til at lykkes. På baggrund af en blanding af beregninger på basis af Newtons gravitationslov, Leonhard Eulers arbejder og erfaringer gjort ved egne minutiøse observationer gennem adskillige år lykkedes det den tyske astronom Tobias Mayer (1723 – 1762) at udarbejde en tabel, som viste sig at kunne fungere.
Hvorledes denne tabel blev udarbejdet, vil vi ikke komme ind på her. En ny og grundig behandling af disse spørgsmål kan findes i Wepster 2010.

 

Hvad måler man?

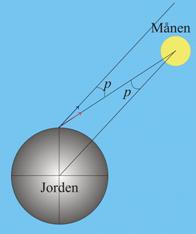
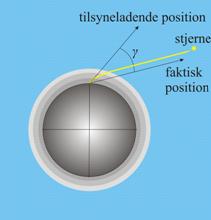
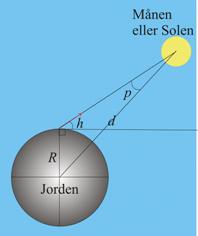
Begrundelsen for glosen månedistance er, at ”måneviserens” position bestemmes ved at måle Månens vinkelafstand på himmelkuglen fra et andet himmellegeme, der kunne være Solen eller en fiksstjerne eller en af planeterne.
Det er imidlertid ikke nok bare at måle denne vinkel, som det fremgår af  tegneserien  Figur 6 til Figur 9 nedenfor.
Det skyldes, at man bliver nødt til at tage hensyn til de to fænomener parallakse og refraktion.

Parallaksen er den vinkel p hvorunder jordradien mellem jordens centrum og observationspunktet ses fra Månens centrum. Det fremgår af  Figur 4 at det er den samme vinkel som Månens tilsyneladende position er forskubbet nedad i forhold til retningen til Månen set fra jordens centrum.

Refraktionen er afbøjning af lyset fra stjernen på grund af passage igennem stadig tættere luftlag. Den bevirker at stjernens tilsyneladende position forskubbes opad med vinklen γ i forhold til den faktiske.

Figur 4. Månens parallakse p.

Figur 5. En stjernes faktiske position og tilsyneladende position på grund af refraktionen.

Månens parallakse er meget større end dens positionsforskydning på grund af refraktion, så Månens refraktion kan negligeres, mens en stjernes parallakse er så lille på grund af den store afstand til stjernerne at man kan se bort fra den i denne sammenhæng og kun regne med  refraktionen.

 

Figur 6. Her ses Månen og en stjerne på himlen over horisonten. For at man kan se horisonten, må det ikke være for mørkt, så målingerne foregår i tusmørket (overgangen mellem dagslys og nattemørke).	Figur 7. Man måler stjernens højde over horisonten v og Månens højde over horisonten w. Dette skal ske omtrent samtidig.
Figur 8. Også samtidig måler man den skrå vinkel u på himmelkuglen mellem stjernen og Månen.	Figur 9. Her ses de tre vinkler man skal måle omtrent samtidig.

Figur 10.

.

Figur 10 viser et moderne (portugisisk) forsøg på at lave en månedistancemåling (mellem Solen og Månen) om bord på et skib. Det illustrerer at der åbenbart er behov for fire personer til at løse opgaven: én til at måle Solens højde over horisonten (manden i forgrunden), én til at måle Månens højde over horisonten (manden i baggrunden), én til at måle den skrå vinkel mellem Solen og Månen (manden der ligger på ryggen på dækket) og endelig én til at notere resultaterne og aflæse klokkeslettet (manden der sidder ved bordet).

 

Sammenhængen mellem nøjagtigheden i måling af månedistancen og nøjagtigheden i bestemmelsen af længdegraden

Månen bevæger sig hele vejen rundt om Jorden på en måned, dvs ca 30 døgn.
(Månens såkaldte sideriske omløbstid er i virkeligheden 27,3 døgn, men vi regner her med det runde tal 30).

Dvs Månen ændrer sin position i forhold til fiksstjernene med ca  pr døgn, hvilket igen vil sige ½ ° pr time. Altså vil afstanden mellem Månen og en given stjerne eller Solen ændre sig ca 30 bueminutter pr time, eller ½ bueminut pr tidsminut.
Hvis vi laver en fejl på x bueminutter i målingen af Månens distance fra en given stjerne eller Solen vil det altså give en fejl i bestemmelsen af det tidspunkt målingen finder sted på 2x tidsminutter.

Hvor stor en indflydelse har så en fejl på 2x tidsminutter på bestemmelsen af længdegradsforskellen?

Jorden drejer sig 360° om sin egen akse på 24 timer, så på 2x tidsminutter vil den dreje sig , hvilket vil sige 30x bueminutter.

En fejl på x bueminutter i målingen af månedistancen vil altså give anledning til en fejl på 30x bueminutter i længdegradsforskellen mellem den aktuelle position og Greenwich. Så enhver fejl i måling af månedistancen vil give en 30 gange så stor fejl i længdegradsforskellen.

Den største dusør udlovet i 1714 var for bestemmelse af længdegraden til søs inden for en margen på 30 sømil. Da 1 sømil er længden af et bueminut på en storcirkel på jorden, vil 30 sømil svare til længden af ½° på en storcirkel. Ved ækvator er det længden af en længdegradsforskel på ½ °.
Den krævede margen er altså på ½ °, dvs 30 bueminutter, så fejlen i målingen af månedistance må ikke være større end 1 bueminut.

 

Parallakse

Man kan finde sammenhængen mellem Solens eller Månens højde over horisonten og parallaksen ved at benytte den trekant på  Figur 11, der har sine vinkelspidser i jordens centrum, observationspunktet og Månens eller Solens centrum. Her er R jordens middelradius og d er middelafstanden til Månen eller Solen.

Figur 11.

Opgave.
Vis at parallaksen p hænger sammen med højden h på følgende måde:
.

Jordens middelradius R = 6368 km. Månens middelafstand fra jorden er d = 384400 km.
Bestem Månens horisontalparallakse, dvs parallaksen svarende til h = 0°.
Lav en tabel over Månens parallakse som funktion af højden h, hvor h varierer fra 0° til 90° med spring på 5°.

Solens middelafstand er 150 millioner km.
Bestem Solens horisontalparallakse og lav en tilsvarende tabel over Solens parallakse som funktion af h.

 

Refraktion (brydning)

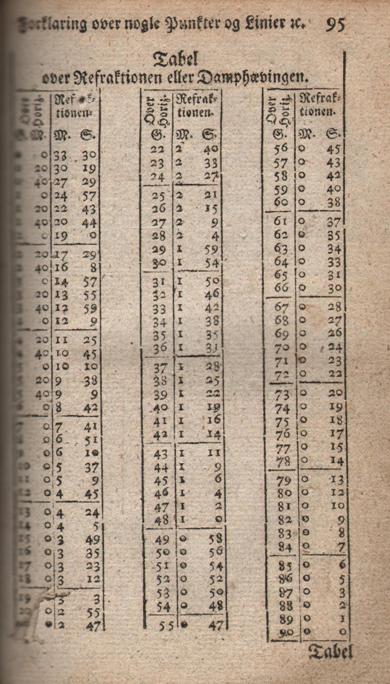
Lysstrålerne fra himmellegemerne brydes i de atmosfæriske lag. Hvis de kommer vinkelret ind på lagene svarende til at himmellegemets højde er 90°, er brydningsvinklen 0°, men ellers bliver brydningsvinklen stadig større, jo tættere luftlag lysstrålerne passerer igennem, og den samlede brydning bliver størst, når himmellegemets højde er 0°, dvs strålerne kommer horisontalt ind mod observationspunktet.
På basis af erfaring og eksperimenter udarbejdede man i 1700-tallet tabeller over refraktionen som funktion af højden.

Et eksempel på en sådan tabel er givet i  Figur 12. Her ses det, at refraktionen for horisontalt indkommende stråler er på 33 ½ bueminut (altså over ½ °), for så at aftage ned mod 0° jo højere himmellegemet kommer på himmelen.

Figur 12. Tabel over refraktionen (anden søjle) som funktion af himmellegemets højde over horisonten (første søjle). Den første søjle helt ude til venstre er lidt tåget, men den begynder med 0° 0’ og fortsætter med spring på 20’. Tabellen er s.95 i Skatkammer eller Styrmands-Kunst, Kiøbenhavn 1781, udgivet af C. C. Lous. [Klik på billedet for at få en forstørret udgave]

Hvad gør man med de målte størrelser?

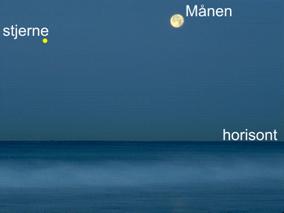
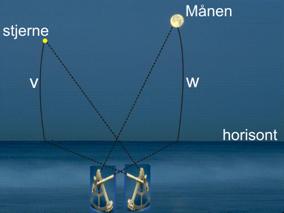
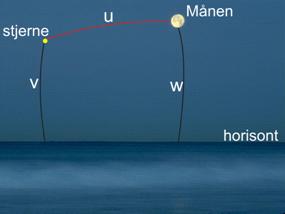
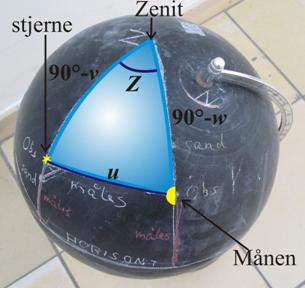
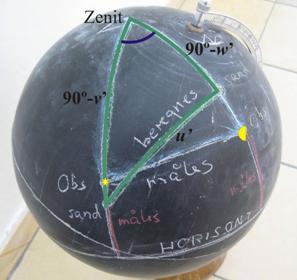
Fremgangsmåden er i det følgende illustreret på en tavleglobus.
Ved en sfærisk trekant forstår man en trekant, hvis sider alle er dele af storcirkler på en kugle.

Den sfæriske trekant, vi i først omgang kigger på, er optegnet med lyseblåt på Figur 13. Dens tre vinkelspidser er zenit (punktet lodret over observatørens hoved), stjernen (eller Solen) og Månen.

Figur 13.

Figur 14.

Vi har målt stjernens højde v over horisonten, Månens højde w over horisonten og den skrå vinkel u mellem stjernen og Månen (som er en bue på den storcirkel på himmelkuglen der går gennem stjernen og Månen).

Figur 15.

Figur 16.

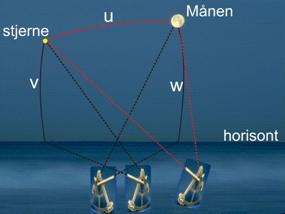
På  Figur 15 vises de stykker af den blå sfæriske trekant, vi dermed har bestemt: Stjernens zenitdistance 90° – v , Månens zenitdistance  90° – w og den målte månedistance u.
Imidlertid skal der jo korrigeres for refraktion og parallakse. Stjernens refraktion bevirker, at dens sande højde over horisonten v’ bliver mindre, mens Månens parallakse bevirker, at dens sande højde over horisonten w’ bliver større (ved Månens sande højde forstår vi vinklen mellem retningen til horisonten og den retning Månen ses i fra jordens centrum).
 

Figur 17.

Figur 18.

De sande zenitdistancer bliver så henholdsvis 90° – v’ og 90° – w’, som det er vist på den grønne trekant på  Figur 17.
På  Figur 18 er vist den grønne sfæriske trekant, hvor den side vi søger er buen u’ på storcirklen mellem stjernens sande position og Månens sande position.

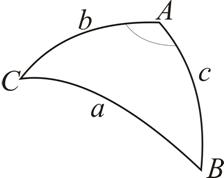
Nu er vi så i stand til ved hjælp af sfærisk trigonometri at beregne u’, når vi kender de nævnte målte størrelser.
Princippet i fremgangsmåden er følgende:

Figur 19.

For den sfæriske trekant vist på Figur 19 gælder der følgende ”cosinusrelation”:     Her er vinkel A vinklen mellem de to planer, som er defineret af de to storcirkler som buerne b og c ligger på.

Nu anvender vi denne formel to gange.

Først på den lyseblå sfæriske trekant:

,
som kan omformes til
.

Dernæst på den grønne sfæriske trekant:

,
som kan omformes til
.

Ved at isolere cos(Z) i de to ligninger, kan vi få

; derved er vinkel Z gået ud af regningerne.

Den eneste ubekendt er her u’, som vi så kan isolere og få

Hvilket jo ser afskrækkende nok ud, men kan dog lade sig udregne uden større besvær på en lommeregner.
I 1700-tallet var sådan en formel imidlertid fuldstændig uhåndterlig. De indgående sinus’er og cosinus’er slog man op i tabeller med fem decimaler, og man skulle så lægge sammen og trække fra og gange og dividere med sådanne mangecifrede tal. Derfor fortsatte man her med at omforme med henblik på at få såkaldte logaritmiske formler, hvor der kun indgik produkter og kvotienter, som man kunne tage logaritmer af. Men det er en længere historie, som vi lader ligge her.

Efter beregning af den korrigerede månedistance

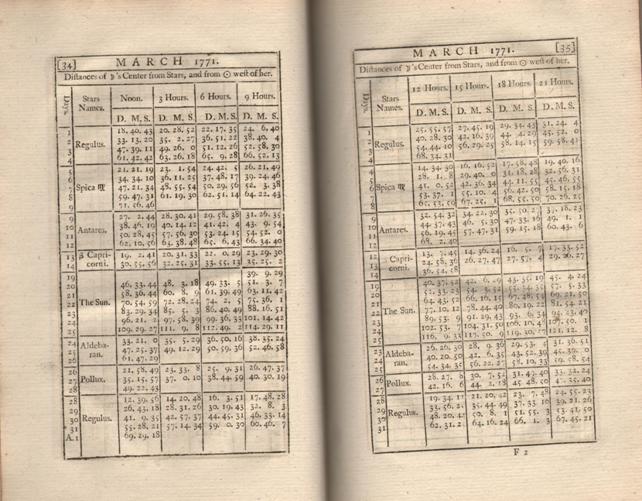
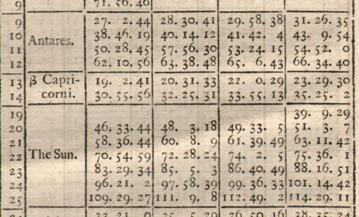
Det sidste man foretager sig efter målingerne og beregningerne er at sammenholde den korrigerede månedistance – der jo altså svarer til at måle vinkelafstanden mellem stjernen eller Solen og Månen set fra jordens centrum – med en tabel over månedistancerne som funktion af klokkeslettet i Greenwich.

Den først tabel af denne art blev udgivet i 1767 under navnet The Nautical Almanac and Astronomical Ephemeris, for the Year 1767. Almanakken blev udgivet af ”The Commissioners of Longitude”, men hovedmanden var den britiske Astronomer Royal, Nevil Maskelyne (1732 - 1811) .Denne almanak blev derefter udgivet hvert år. Samtidig udgav Maskelyne også nogle tabeller, som ikke behøvede at blive fornyet hvert år, disse udkom under titlen Tables Requisite to be Used with the Astronomical and Nautical Ephemeris. Det var heri, man bl.a. kunne finde tabeller over refraktion og parallakse.

Man kan få et indtryk af den relevante tabels indretning ved at se på et enkelt opslag i udgaven for 1771:

Figur 20. Opslag på tabellen over ”Distances of |) Center from Stars, and from ͽ west of her” – her er |) tegnet for Månen og ͽ tegnet for Solen. Opslaget dækker marts måned 1771 og har månedistancer for Solen og syv forskellige stjerner. Hvilke stjerner der står angivet på hvilke datoer afhænger af om de ses samtidig med Månen på himmelen og om det er nogenlunde bekvemt at måle distancen. [Klik på billedet for at få en forstørret udgave]

Figur 21. Detalje fra tabelopslaget. Her ses, at når man måler månedistancer fra Solen risikerer man at komme et stykke over 90 grader.

Hvilke instrumenter målte man vinklerne med?

Udviklingen af månedistancemetoden betød samtidig en udvikling af håndholdte vinkelmålingsinstrumenter; til søs kunne man jo ikke så godt bruge instrumenter der skulle stilles vandret på et stativ. Indtil omkring 1730 måtte man klare sig med jakobsstav, daviskvadrant eller søastrolabium og ingen af disse kunne blot tilnærmelsesvis måle vinkler med den præcision som krævedes i månedistancemetoden.

Fra 1730’erne fik havde man imidlertid et langt bedre instrument, oktanten. Samtidig med at astronomerne, først og fremmest Tobias Mayer, arbejdede med at få udarbejdet tabeller over Månens bevægelse med stadig større nøjagtighed, arbejdede instrumentmagerne med at konstruere oktanter med bedre og bedre skalaer, så man kunne nærme sig det afgørende mål, nemlig at kunne måle med en nøjagtighed på 1 bueminut. Dette var jo en betingelse for at kunne bestemme længdegraden inden for den margen, som The Longitude Act forlangte.

Som omtalt tidligere kan man risikere at skulle måle en månedistance der er over 90°. En oktant kan kun måle vinkler mellem 0° og 90°, så her måtte man videreudvikle instrumentet. Tobias Mayer havde foreslået et instrument med en skala på en hel cirkel og havde også fabrikeret en prototype i træ og sendt til England (igen som en del af jagten på dusøren!) for at få den berømte instrumentmager John Bird til at fabrikere den mere professionelt i metal. Dette skete også, men ved forsøgene med instrumentet i den engelske flåde fandt officererne instrumentet for klodset og besværligt at bruge. I stedet foreslog man en udvidelse af skalaen på oktanten, og således blev sekstanten født. Sekstanten kan måle vinkler mellem 0° og 120°.

Det blev sekstanten som i de følgende årtier slog igennem som standardvinkelmåleren til søs for de skibe og søfolk, der havde råd til at anskaffe instrumentet. Sekstanten var stadig meget dyrere end de gamle træinstrumenter jakobsstav og daviskvadrant, og disse blev da også fremstillet endnu et stykke ind i 1800-tallet. Efterhånden blev sekstanten sat i masseproduktion og derved faldt prisen.

 

Månedistancemetodens endelige nederlag i konkurrence med kronometermetoden

Til gengæld var det instrument, der skulle bruges i den metode der konkurrerede med månedistancemetoden, i lang tid meget, meget dyrere end sekstanten. Det var kronometeret, søuret, som den geniale håndværker John Harrison igennem et langt liv udviklede til et instrument, der kunne måle tiden med en nøjagtighed og pålidelighed, der stod mål med kravene i Act of Longitude. På grund af kronometrets kostbarhed var månedistancemetoden endnu i adskillige årtier ind i 1800-tallet en brugt metode ved oceansejlads og en metode der blev undervist i på søofficersskolerne. Eksempelvis er der omhyggeligt gjort rede for metoden i brødrene Tuxens navigationslærebog for søkadetter, der udkom i 1856[1] [se uddrag] . Den krævede dog et ret højt niveau i forståelse for astronomi og matematik.

I anden halvdel af 1800-tallet ebber brugen af metoden ud og skibskronometre bliver efterhånden en del af standardudstyret på langt de fleste skibe. Med opfindelsen af radiosignalet som et nyt middel ved siden af kronometret til at bestemme tidsforskelle til søs og dermed længdegradsforskelle går metoden over til at være en sport for særligt interesserede. Det var dog først i 1906 at The Nautical Almanac holdt op med at bringe de tabeller, der skulle bruges i forbindelse med månedistancemetoden.

Litteratur

The Nautical Almanac and Astronomical Ephemeris, for the Year 1767 and Tables Requisite to be Used with the Astronomical and Nautical Ephemeris findes på elektronisk form her:
http://books.google.com/books/about/THE_NAUTICAL_ALMANAC_AND_ASTRONOMICAL_EP.html?id=8f4NAAAAQAAJ

Steven A. Wepster: Between Theory and Observations. Tobias Mayer’s Explorations of Lunar Motion, 1751 – 1755. Springer 2010.

Wikipedia har en pålidelig artikel om månedistancemetoden: http://en.wikipedia.org/wiki/Lunar_distance_%28navigation%29  - her er også flere links og litteraturhenvisninger.

Sidst revideret 8. november 2011