|
Om bestikregning
Download dette dokument i
Word-format
Download dette dokument i pdf-format
Bestikregning går ud på, at man forsøger at finde ud af
hvor man er ved at benytte sig af følgende oplysninger:
a. Udgangspunktets position
(breddegrad og længdegrad)
b. Hvilken retning har vi sejlet i?
c. Hvor langt har vi sejlet?
I princippet vil man så kunne besvare spørgsmålet: hvor er
vi nu?
I praksis er dette svar forbundet med en lang række fejlkilder og usikkerheder.
Det har derfor fra de allertidligste rejser på oceanerne været et stort ønske at
kunne kontrollere resultatet af bestikregningen ved uafhængige målinger.
Hvordan foretages bestikregning?
Vi går ud fra, at vi kender udgangspunktets position – det
kunne f.eks. være en europæisk havn.
Retningen (kursen)
Retningen kan bestemmes ved at orientere sig efter verdenshjørnerne;
hvis vi kender retningen til nord, kan vi fastlægge skibets kurs i
forhold til denne retning. Siden magnetkompasset kom til Europa fra Kina omkring
1100 har man kunnet bestemme retningen til nord uafhængigt af vejrforholdene.
Retningen har traditionelt været angivet ved kompasretningsangivelser. Disse har
betegnelser som vist på fig. 1, der stammer fra en styrmandslærebog fra
slutningen af 1700-tallet.
Som det ses, er kompasskiven inddelt i ialt 32 retninger, 8 fra nord til øst, 8
fra øst til syd, 8 fra syd til vest og 8 fra vest til nord. Disse retningers
navne angives med ord, som f.eks. med udgangspunkt i nord: nord til øst, nord
nordøst, nordøst til nord, nordøst (som er lige midt mellem øst og nord),
nordøst til øst, øst nordøst, øst til nord og øst. De 90 grader mellem øst og
nord er således inddelt i 8 lige store dele, således at de angivne retninger kan
omregnes til grader. Dette får man brug for, når man skal lave egentlige
bestikberegninger.
Fejlkilder: Der er to vigtige:
- Kompasnålen peger mod den magnetiske sydpol, som ligger
et stykke fra den geografiske nordpol, og som oven i købet flytter sig med
tiden. Denne fejl har man lavet tabeller over for at kunne rette den. Fejlen
kaldes misvisningen.
- Skibet indeholder en del jern, som vil få magnetnålen
til at vise forkert. Denne fejl kan man tage hensyn til ved at måle den, når
man kender den rigtige retning til geografisk nord. Fejlen kaldes
deviationen.
Distancen
Dernæst skal vi bestemme hvor langt vi har sejlet den såkaldte udsejlede
distance.
Dette kan gøres ved at bestemme farten og gange denne med længden af den tid
skibet har sejlet i.

Figur 1.
Kompasretningerne. [C.C. Lous: Styrmands-Kunst eller saa kaldet Skatkammer,
Kiøbenhavn 1787, s.234]
(Klik på figuren for at få større billede)
Farten måles f.eks. i sømil pr time (som kaldes knob)
og når man så ganger med det antal timer skibet har sejlet fås distancen målt i
sømil. Betegnelsen knob stammer fra det instrument, man har brugt til at bestemme
farten med. Oprindelig har det blot været et træstykke eller lignende man smed i
vandet, hvorpå man så målte hvor lang tid det tog om at passere fra et mærke på
skibet til et andet. Senere bandt man et reb i træstykket og lod rebet løbe ud i
et nøje afmålt tidsrum (målt på et timeglas, hvor sandet løber igennem på f.eks.
28 sekunder); på rebet var der bundet nogle knuder, knob, med
regelmæssige mellemrum og på den måde kunne man måle hvor langt et stykke reb
der var løbet ud i det angivne tidsrum.
Fejlkilder: Der kunne være fejl forbundet med timeglasset, som skal vendes
præcist når tællingen af antal knob begynder, og der kommer fejl, hvis farten
ændres undervejs. Derfor er det vigtigt at måle farten ofte, så der kan tages
hensyn til variationer.
Resultatet: nuværende position
Nu kan man så foretage en egentlig beregning af hvor man befinder sig.
Man kan angive resultatet ved hvor mange sømil man befinder sig syd eller nord
for udgangspunktet og hvor mange sømil man befinder sig øst eller vest for
udgangspunktet. Dvs man opløser skibets tilbagelagte strækning i to, en ren
nord-syd-gående og en ren øst-vest-gående, som vist på fig. 2, hvor
udgangspunktet er A og slutpunktet er B. På den måde får man en retvinklet
trekant.
Det er nu en nødvendig forudsætning, at afstandene vi taler om er så små, at vi
kan regne dem for linjestykker i en plan; i virkeligheden er de jo buestykker på
en kugle.
|
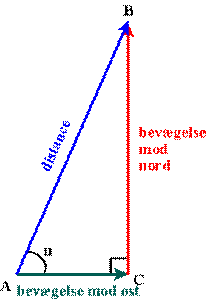
Figur 2 |
 |
På den måde kan man angive slutpunktets position ved at
sige hvor mange sømil vi befinder os øst for A og hvor mange sømil vi befinder
os nord for A.
Men hvis vi kender udgangspunktets position ved dets breddegrad og længdegrad,
vil vi også gerne kunne angive slutpunktets position ved dets breddegrad og
længdegrad. Kan vi beregne os til det?
Ja, for breddens vedkommende kan det nemt lade sig gøre.
Én sømil er nemlig defineret til at være gennemsnitslængden af et bueminut på en
storcirkel på jordens overflade. Og da bredden måles på den meridian, der går
gennem B, vil bevægelsen mod nord i sømil simpelthen svare til en ændring i
bredde på et tilsvarende antal bueminutter.
Så hvis f.eks. strækningen BC er 72 sømil, har skibet ændret sin bredde med 72
bueminutter mod nord, dvs. 1 grad og 12 bueminutter. Hvis man så ved at A
befinder sig på 44 grader og 40 bueminutters nordlig bredde, må B altså ligge på
45 grader og 52 bueminutters nordlig bredde.
Hvad længden angår stiller sagen sig anderledes.
Problemet er, at AC ikke er et stykke af en storcirkel (sådan som BC), men
derimod et stykke af en breddecirkel, der er en lillecirkel med centrum på
jordens omdrejningsakse, medmindre A og C da befinder sig på ækvator.
Vi kan derfor ikke uden videre omregne længden af AC i sømil til AC i
bueminutter. Omregnings-faktoren vil afhænge af hvor langt fra ækvator vi
befinder os. Dette problem begyndte man allerede at tumle med i 1500-tallet og
man fik efterhånden udarbejdet tabeller over hvor langt et længdebueminut er
afhængigt af hvilken bredde man befinder sig på. Ved ækvator er det netop 1
sømil, da ækvator er en storcirkel, ved 30 graders bredde (nordlig eller sydlig)
er bueminuttet 0,87 sømil, ved 60 graders bredde er det 0,5 sømil og ved
polerne svinder det ind til 0 sømil.
I William Bourne: A Regiment for the Sea, London 1574 angives en geometrisk måde
at bestemme længden af en længdegrad på. Senere kommer egentlige tabeller, som
f.eks. tabellen på fig. 3-4.
(Begge tabeller kan ses i større format ved at
klikke her)
|
|
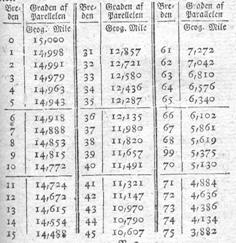
Figur 3. Tabel over længden af en længdegrad på en given parallelcirkel. [Bugges
Astronomi, 1796, s. 259] |
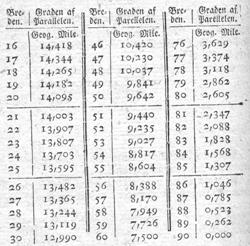
Figur 4.
Tabellens fortsættelse [s.260]
|
Den viste tabel angiver længden af en længdegrad i
geografiske mil. En geografisk mil er 4 sømil.
Så det kan f.eks. ses af tabellen, at ved 55 graders nordlig bredde er en
længdegrad 8,604 geografiske mil dvs. 34,416 sømil, mens den ved ækvator er 60
sømil.
Med en rimelig detaljeret tabel til rådighed kan det altså lade sig gøre også at
beregne, hvor meget længden er ændret.
Astronomisk kontrol
Den ideelle situation for en styrmand der foretager bestikregning vil være
at få bekræftet beregningen ved målinger, der er uafhængige af beregningen. For
breddens vedkommende kan det lade sig ved at foretage passende vinkelmålinger på
himmelkuglen som beskrevet i skriftet Navigation. For længdens
vedkommende var det i århundreder en håbløs opgave; man var klar over siden
1500-tallet at det var et spørgsmål om at kende tidsforskellen, men det var
tilsyneladende et uløseligt problem, i hvert fald hvis man skulle have svaret
med en nøjagtighed, der kunne bruges til noget til søs.
I 1700-tallet var man kommet så langt med den astronomiske forskning, at man
kunne udvikle en metode der i princippet kunne bestemme længdeforskellen
astronomisk, nemlig den såkaldte månedistancemetode. Samtidig arbejdede
englænderen John Harrison på at konstruere et ur, der var tilstrækkelig stabilt
og gik tilstrækkelig nøjagtigt til at det kunne medtages om bord på et skib og
under flere måneder lange rejser vise klokkeslettet hjemme i London. De to
metoder stod længe som ligeværdige konkurrenter. Ulempen ved de nøjagtige ure,
kaldet kronometre, var længe at de var meget dyre i anskaffelse, mens
månedistancemetoden blot krævede en sekstant, men i det lange løb sejrede urene
alligevel. Op igennem 1800-tallet blev det stadig mere almindeligt at skibe
medbragte kronometre, og i slutningen af århundredet døde månedistancemetoden
hen og blev en metode der kun havde historisk interesse.
Konkret
eksempel på bestikregning fra 1795:
Grodtschillings navigationsbog,
kap. 22, eks. 1.
|



