Beregning af længdeforskel ved bestikregning

Download dette dokument i Word-format
Download dette dokument i pdf-format

Bestemmelsen af længdegraden er vanskeligere end bestemmelsen af breddegraden, fordi der skal bruges meget præcist gående ure. Peter Freuchen beskriver i sin videnskabelige rapport Meteorological Observations hvilke problemer han har haft med urene og ender med at skrive

Our determinations of longitude on the inland ice are therefore based for the most part on the distances covered, these being determined by means of an odometer, marking tenths of a kilometre. I have both on this and previous trips had occasion to note that the error involved – when travelling with sledges drawn by dogs, and according to compass, – by taking 2 kilometres’ run as = one mile ( = 1 minute) in a straight line, is practically imperceptible.

Det han antyder her, er at han I virkeligheden tyr til den såkaldte bestikregning, der har været anvendt til søs i århundreder til at finde et overslag over hvor meget længden har ændret sig siden sidste positionsbestemmelse.

Her kommer en kort beskrivelse:

Bestiktrekanten

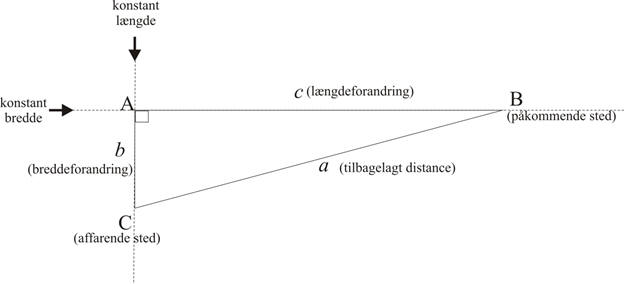
Den sidste position (C)  kaldes i sømandssproget ”det affarende sted” og den position vi gerne vil finde bredde og længde for (B) kaldes ”det påkommende sted”.
Vi regner med at afstandene er så små at vi uden at begå større fejl kan betragte bestiktrekanten som en plan, retvinklet trekant.

Bredden for C og bredden for B findes ved udregning på basis af zenitdistanceobservationer. Dermed kan vi også finde breddeforandringen, som er længden af siden AC målt i bueminutter. Nu er længden af et bueminut på en storcirkel netop 1 sømil (1.852 km), så vi kan let finde længden af AC i sømil.
Peter Freuchen skriver i det ovenfor citerede, at han benytter en tommelfingerregel, der siger at 1 sømil er 2 km (i stedet for 1.852 km). Det gør han fordi hodometeret angiver den tilbagelagte distance i km, og hundeslæden bevæger sig ikke nødvendigvis i en snorlige linje, så for at tage højde for det omregner han på den måde den tilbagelagte distance (CB) til et lidt lavere antal sømil.

Nu kender vi både kateten CA og hypotenusen CB i den retvinklede bestiktrekant og kan således let beregne den sidste katete AB. Det er netop længdeforandringen, som vi så får beregnet i sømil.

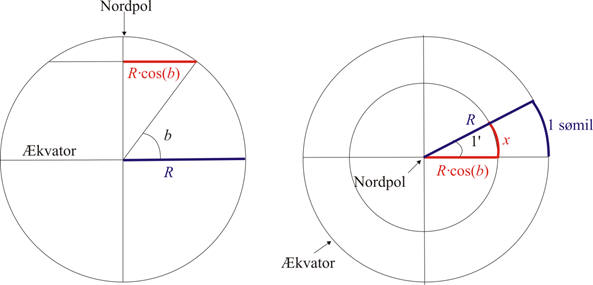
Men vi er interesseret i længdeforandringen i bueminutter. AB er del af en lillecirkel og ikke en storcirkel på jordkloden, så vi kan ikke uden videre oversætte sømil til bueminutter. Hvad så?

Vi ser på følgende tegning:

Tegningen til venstre viser jordkloden set fra siden. Jordens radius kaldes R. Hvis bredden er b, er radius i breddeparallelcirklen R cos(b). Tegningen til højre viser jordkloden set fra oven. Der er vist en vinkel på 1 bueminut (voldsomt overdrevet på tegningen!). På ækvator har buen svarende til denne vinkel en længde på 1 sømil, men på breddeparallelcirklen har den længden x = 1 sømil ∙ cos(b). Jo større b bliver, jo mindre bliver x. Hvert bueminut har altså længden  1 sømil ∙ cos(b) på breddeparallellen svarende til bredden b. Vi får derfor følgende omsætningsformel: Den bredde b, vi skal regne med i omsætningsformlen, er middelbredden mellem bredden for C og bredden for B. På den måde kan vi bestemme AB i bueminutter og dermed har vi fundet længdeforskellen.   OPGAVE Find længdeforskellen mellem lejr VII og lejr VIII ved bestikregning. Hvis Peter Freuchens overslag over længden for lejr VII er korrekt, hvad er så længden for lejr VIII?