|
*********************************************************************
Nu efterfølger adskillige Exempler med hos antegnede
Figurer / huilcke klarligen udvijser den rette
Undervijsning oc Forklaring paa forskreffne Reguler.
I. Exempel oc Figur til den Første Regula naar
Solen haffver Sydlig Declination.
 I
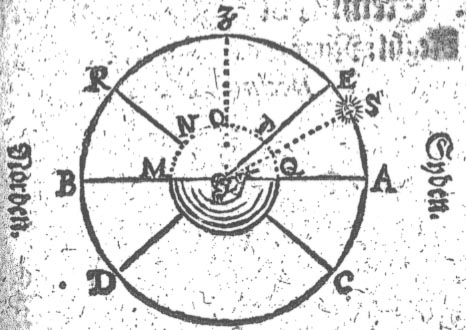
denne Figur lad B.R.Z.E.A.C.D. betegne Meridianen. R. Nord-Polen
/ oc C. Sønder-Polen. D.E. Æqvinoctialen. Z. Zenith, oc
M.N.O.P.Q. Jorden. B.A. Horizonten. I
denne Figur lad B.R.Z.E.A.C.D. betegne Meridianen. R. Nord-Polen
/ oc C. Sønder-Polen. D.E. Æqvinoctialen. Z. Zenith, oc
M.N.O.P.Q. Jorden. B.A. Horizonten.
Nu tager jeg Solens Høyde offver Horizonten /
som fra A til S 30 Grad. oc SE Sydlig Declination 4 Grad. 5 Min.
Nu addêrer jeg SE 4 Grad. 5 Minut til AS 30
Grader / da bekommer jeg for AE 34 Grader / 5 Min. som er Æqvinoctialens
Høyde udi Sønden. Dennem tager jeg
fig. 9
nu fra A.Z. 90 Grad. Da resterer for EZ 55 Grad. 55 Min. som er
den Distantz imellom min Zenith oc Æqvinoctialen /
som oc kommer offver ens med Plassen Norden Æqvinoctialen paa
Jorden. PO eller oc med Nord-Polens Høyde offver Horizonten i
Norden BR.
II. Exempel oc Figur til den Første Regul: Naar Solen
haffver Nordlig Declination.

I denne Figur er B.P.E.A.C.D. Meridianen. E.D.
ÆqviPoctialen [sic!]. A.S. 60 Grader som er Solens eller en Stiærnis
rette Høyde offver Horizonten. Oc dens Nordlig Declination
E.S. er 11 Grader.
Nu subtrahêrer E.S. Declinationen /
som er 11 Grader fra Solens Høyde A.S. som er 60 Grad. Da
offverbliffver for A.E. 49 Grader / som er da Æqvinoctialens Høyde
i Sønder.
fig. 10
Dennem tager jeg fra E.A. 90 Grader / oc bliffver da igien 41 Grader for
A.C. Saa vijt er Syd-Polen under Horizonten / huilcken Distantz
er lig med B.P. Nord-Polens Høyde offver Horizonten; Er endog
lig med E.Z. min Zeniths Plass Norden Æqvinoctialen.
Huilcken Distantz kommer overens med Latitudinem eller
Bredden paa Jorden / som er min Distantz fra Æqvinoctialen
I. til K.
III. Exempel oc Figur til den Første Regul / naar Zenith
er ret udi Æqvinoctialen.
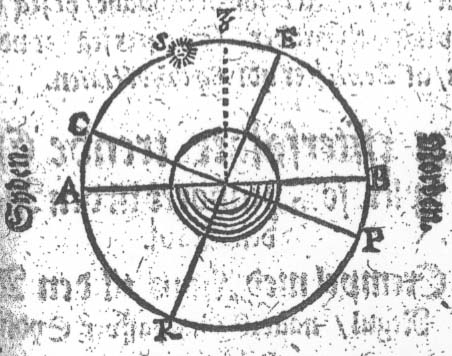
End være udi denne Figur / at E.R. er Æqvinoctialen
/ oc A.S. Solen rette Høyde udi Sønden 82 Grader / E.S. Solens sydlig
Declination 20 Grader.
Nu adderer jeg Solens Declination E.S.
20 grader tilderis Høyde A.S. 82 Grader / oc jeg bekommer da A.E. 102
Grad. herfra tager jeg den siden 90 Grad. A.Z. oc mig rester igien Z.E.
12 Grad. da er Æqvinoctialen saa langt under Zenith i
Norden. Her aff slutter jeg / at Nord-Polen
fig. 11
P. er ocsaa lige saa megit under den Norden Horizont B. oc
Syd-Polen C. er lige saa mange Grader offver den SØnder Horizont
A.
Men dersom Solens Høyde er som tilforne 82 Grader /
oc dens Declination er 8 Grad. Da adderer jeg dem tijhaabe
/ oc jeg bekommer lige 90 Grader. Saa jeg der udi Figuren / at Zenith
er udi Æqvinoctialen.
Nu effterfølger trende Exempler / som henhører til
den Anden Regul.
I. Exempel med Figur til den Anden Regul / naar Solen
haffver Sydlig Declination.
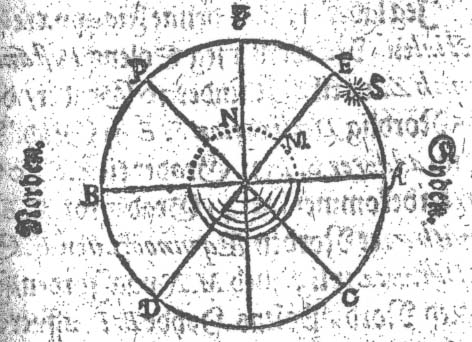
I denne Figur lader jeg Solens Distantz fra Zenith
være S.Z. 50 Grader / oc dens Sydlig Declination S.E. 11 Grader.
Nu subtrahêrer jeg S.E. 11 Grader fra S.Z. 50
Grader. Da rester igien E.Z. 39 Grad.
oc saa meget er Zenith Z. Norden for Æqvinoctialen
E. Oc er samme Distantz lige med M.N. paa Jorden / sampt oc
Polens Høyde Norden offver Horizonten P.B.
fig. 12
II. Exempel oc Figur til den Første Regul: Naar Solen
haffver Nordlig Declination.
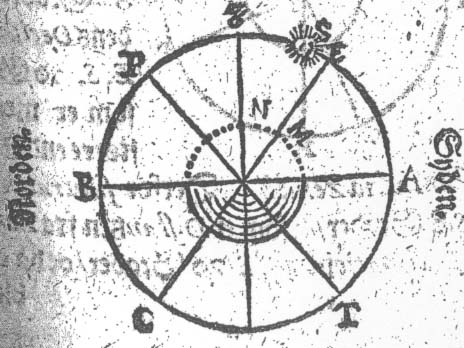
Jeg lader E.C. i denne Figur være Æqvinoctialen.
Nu maaler jeg Solens Distantz fra Zenith Z. oc til S. oc
finder 30 Grader / oc Solens Nordlig Declination S.E. 11 Grad.
Naar jeg nu adderer S.E. 11 Grader til Z.S. 30 Grader / da
bekommer jeg 41 Grader for Z.E. som Zenith Z. er Norden Æqvinoctialen
E. Samme Distantz er lig med M.N. paa Jorden / sampt oc med
Nord-Polens Høyde B.P. offver Horizonten.
fig. 13
III. Exempel oc Figur til den Anden Regul.
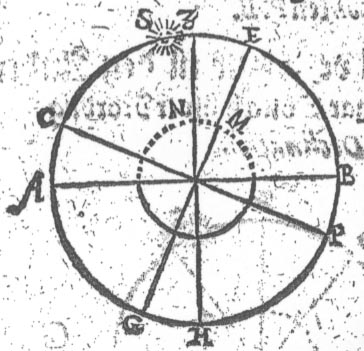
I denne Figur er Solen Distantz fra Zenith
som fra Z. til S. 8 Grader / oc dens Declination E.S. 20 Grader
som er meere oc større end Solens Distantz fra Zenith.
Derfor subtrahêrer jeg Z.S. 8 Grader / (som er Distantz
fra Zenith) fra Declinationen S.E. 20 Grader / oc da
ofverbliffver Z.E. 12 Grader. Oc saa meget er Æqvinoctialen E.
neden for Zenith Z. i Norden. Der aff seer jeg / at Nord-Polen P.
er ocsaa 12 Grader under den Norder Horizont B. oc tuert imod er
Syd-Polen C. lige saa mange Grader offver Horizonten A. udi Sønden.
fig. 14
Dersom Solens Distantz fra Zenith, som
fra S. til Z. vaar 8 Grader / ligesom Declinationen. Da sluttede
jeg der aff / at Zenithen Z. er ret lige udi Æqvinoctialen
/ foruden nogen Forskiel.
Følger nu Trende Exempler / som hører til den Tredie
Regul.
I. Exempel til den Tredie Regul / naar Declinationen
er Sydlig.
I denne Figur maa C. være Syd-Polen oc P.
Nord-Polen; D.E. Æqvinoctialen. A.B. Horizonten. Z. Zenith,
oc M.H.I.K.L. Jorden.
Nu lader jeg A.S. være Solens Høyde offver Jorden /
eller Horizonten i Norden / som er 58 grader / oc D.S. dens
Sydlig Declination 8 Grader.
Naar jeg nu subtrahêrer D.S. 8 Grader fra
A.S. 58 grader. da rester forneffnde A.D. 50 grader / huilcket er Æqvinoctialens
Høyde
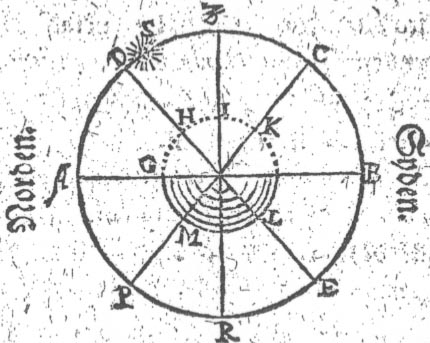 offver
Horizonten. Samme 50 Grader subtrahêrer jeg atter igien
fra 90 Grader D.P.; da offverbliffver igien for A.P. 40 Grader / oc saa
meget er Nord-Polen under Horizonten. Huilcken Distantz er
lige med Syd-Polens Høyde i Sønden B.C. som jeg søgte. offver
Horizonten. Samme 50 Grader subtrahêrer jeg atter igien
fra 90 Grader D.P.; da offverbliffver igien for A.P. 40 Grader / oc saa
meget er Nord-Polen under Horizonten. Huilcken Distantz er
lige med Syd-Polens Høyde i Sønden B.C. som jeg søgte.
fig. 15
II. Exempel til den Tredie Regul / naar Declinationen
er Nordlig.
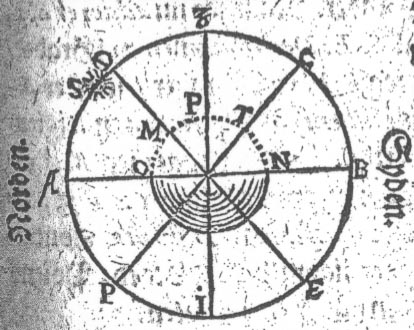 I
denne Figur er D.E. Æqvinoctialen. A.S. Solens Høyde i Norden
39 Grader / oc S.D. Nordlig Declination 14 Grad. I
denne Figur er D.E. Æqvinoctialen. A.S. Solens Høyde i Norden
39 Grader / oc S.D. Nordlig Declination 14 Grad.
Naar jeg nu addêrer Declinationen S.D.
14 grader til A.S. Solens Høyde 39 Grader
Da bekommer jeg 53 Grader for Æqvinoctialens
Høyde. Dennem subtrahêrer jeg fra D.P. 90 Grader / da
offverbliffver A.P. 37 Grader / huilcken Distantz er lige med
Syd-Polens Høyde C.B. eller oc M.P. Breden fra Æqvinoctialen
paa Jorden.
fig. 16
III. Exempel oc figur til den Treide Regul
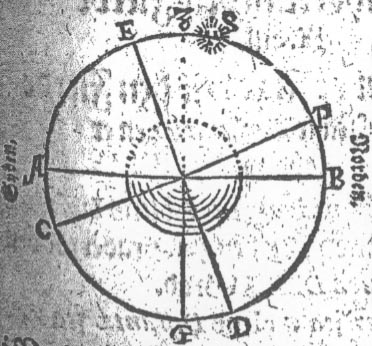
I denne Figur er E.D. Æqvinoctialen. A.B. Horizonten.
C. Syd-Pol / P. Nord-Pol. Nu siger jeg / at B.S. er Solens Høyde i
Norden 82 Grader / oc den Nordlig Declination E.S. 21 Grader.
Naar jeg nu addêrer S.B. 82 Grader til S.E. Declinationen
21 Grader / de bekommer jeg B.E. 103 Grader / som er Æqvinoctialens
Distantz fra Horizonten B igiennem Zenith Z. til E.
Siden tager jeg B.Z. 90 Grader her fra / oc der offver bliffver Z.E. 13
grader / som er Æqvinoctialens Distantz Sønden fra Zenith
/ oc er lig med B.P. Nord-Polens Høyde i Norden offver Horizonten.
fig. 17
Men dersom Solen Høyde B.S. er 82 Grader / oc Declinationen
E.S. 8 Grader. Da seer jeg aff denne Figur / at Æqvinoctialen er
ret udi Zenith.
Følger nu trende Exempler / som henhører til den
Fierde Regul.
I. Exempel oc Figur til den Fierde Regul; Naar Declinationen
er Sydlig.
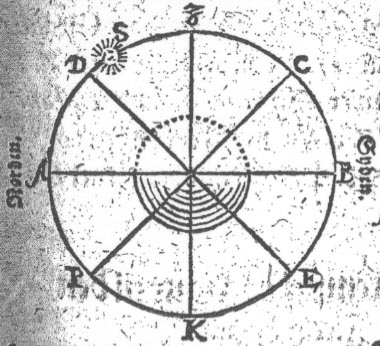 I
denne Figur tager jeg Solens Distantz Z.S. fra Zenith mod
Norden 32 Grader / oc den Sydlig Declination D.S. 8 Grad. I
denne Figur tager jeg Solens Distantz Z.S. fra Zenith mod
Norden 32 Grader / oc den Sydlig Declination D.S. 8 Grad.
Nu addêrer jeg Solens Distantz fra Zenith
Z.S. 32 Grader til Solens.Declination
8 Grader D.S. Da bekommer jeg Z.D. 40 Grader / som er
den Plass oc Distantz som min Zenith er Sønden for Æqvinoctialen
D. huilcken er lige med B.C. Syd-Polens Høyde i Sønden offver Horizonten.
fig. 18
II. Exempel til den Fierde regul; Naar Declinationen
er Nordlig.
 I
denne Figur er A.B. Horizonten, D.E. Æqvinoctialen / C.
Syd-Pol / oc F. Nord-Pol / Z. Zenith. I
denne Figur er A.B. Horizonten, D.E. Æqvinoctialen / C.
Syd-Pol / oc F. Nord-Pol / Z. Zenith.
Nu er Solens Distantz fra Zenith Z.S.
51 Grader udi Norden / oc dens Nordlig Declination D.S. 14
Grader.
Naar jeg da subtrahêrer D.S. 14 Grader / fra
Z.S. 51 Grader / da offverbliffver for Z.D. 37 Grader / som er Æqvinoctialens
Distantz udi Norden fra Zenith, huilcket kommer offverens
med B.C. Syd-Polens Høyde Horizonten.
fig. 19
III. Exempel oc Figur til den Fierde Regul
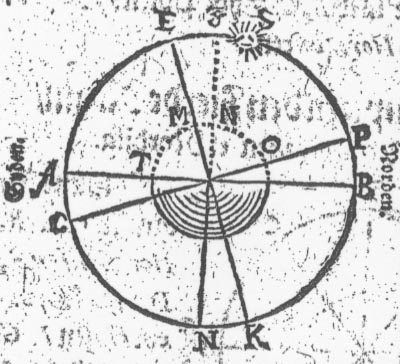
I denne Figur tager jeg Solens Distantz fra Zenith
Z.S. 8 Grad. i Norden; Oc dens Nordlig Declination E.S. 21
Grader.
Nu er Declinationen meere oc større end Distantzen
/ derfor subtrahêrer jeg Solens Distantz fra Zenith
Z.S: 8 Grader fra Declinationen S.E. 21 Grader / da bliffver der
igien for Z.E. 13 Grader / som Zenith er Norden Æqvinoctialen
/ huilcket kommer oc lige offverens met B.P. Nord-Polens Høyde offver Horizonten.
fig. 20
Men dersom Solens Declination haffde været 8
Grader i steden for Solens Distantz fra Zenith som Z.S, da
var det klarligt nok at slutte aff Figuren / at Æqvinoctialen
vaar ret lige udi Zenith Z.
Anfangende den Femte Regul giøris da icke fornøden
/ at jeg den med Exempler oc Figurer skal demonstrêre effterdi
at alle Omstendigheder der udi ere klare nock udi sig selff / oc behøffver
derfor ingen Forklaring.
Exempel oc Figur til den Siette Regul.
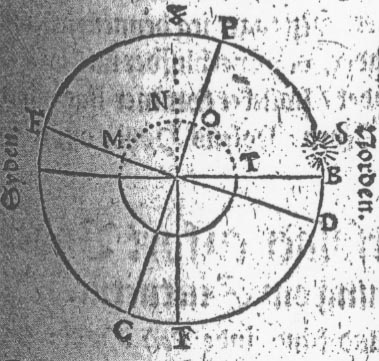 I
denne Figur er P. nord-Pol / oc C. syd-Pol / E.D. Æqvinoctialen
/ S. Solen / Oc B.S. Solens Høyde offver Horizonten. I
denne Figur er P. nord-Pol / oc C. syd-Pol / E.D. Æqvinoctialen
/ S. Solen / Oc B.S. Solens Høyde offver Horizonten.
Nu er samme Solens Høyde 8 Grader / D.S den Nordlig Declination
18 Grader / oc er dens Complement 72 Grader.
Derfor addêrer jeg Solens Høyde B.S. 8
Grader til dens Complement 72 S.P. Grader / da bekommer jeg 80
Grader / som er Høyden aff Nord-Polen / som kommer offverens med E.Z.
som Zenith Z. er Norden for Æqvinoctialen.
fig. 21
Exempel paa den Siuffvende Regul
Udi forgangen Figur lader jeg S. betegne Solens Distantz
fra Zenith 82 Grader / S.D. Solens Norder Declination 18
Grader. Naar jeg nu effter Regulen addêrer S.D. 18 grader til
Z.S. 82 Grader / da bekommer jeg 100 Grader. Nu tager jeg dennem atter
fra Z.F. 180 Grader / oc offverbliffver mig da igien D.F. 80 Grader /
huilcket kommer lige offverens med B.P. Nord-Polens Høyde offver Horizonten.
|
 om
tilforne er formeldet. Huilcket er saa meget klarliger sagt: Lige saa høyt
som Polen ofver Horizonten; saa vijt er altid din Zeniths Distantz
fra Æqvinoctialen.
om
tilforne er formeldet. Huilcket er saa meget klarliger sagt: Lige saa høyt
som Polen ofver Horizonten; saa vijt er altid din Zeniths Distantz
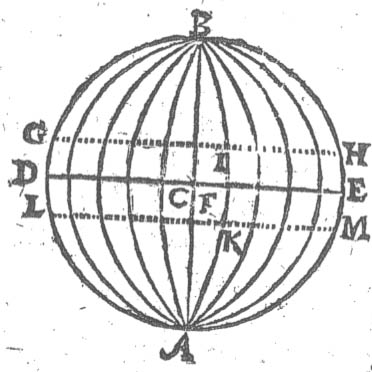
fra Æqvinoctialen.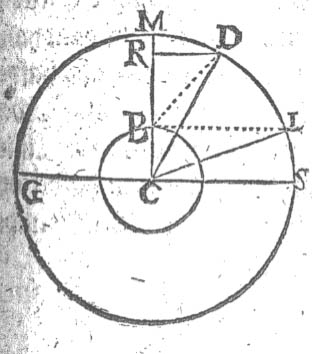 Udi
denne Figur betegner B. Jordens Kugel. C. Jordens Centrum eller
Middelpunckt. B.L. den siunlig Horizont. G.M.D.L. Meridianens
Circul, igiennem huilcken Solen hafver sit Lob; Naar nu Solen er udi Zenith
M. da findis der ingen Parallaxis eller Wlighed aff deris Siun /
baade den som staar paa Jorden / oc den som staar (om mueligt var) udi
Jordens Centro eller Middelpunckt / fordi de seer da begge lige
op offver deris Hoffvet. Men dersom Solen var i D. da kunde den
Nederligere sees aff den som stod offven paa Jorden i B. end aff den som
stod i Jordens Centro C. Oc den Forskiel oc Wlijhed aff deris
Siun / som actis udi den Angulo eller Vinkel B.D.C kaldis Solens Parallaxis.
Jo nærmeere Solen kommer til Horizonten / jo meere Forskiel er
der paa / oc jo større bifver hendis Parallaxis.
Udi
denne Figur betegner B. Jordens Kugel. C. Jordens Centrum eller
Middelpunckt. B.L. den siunlig Horizont. G.M.D.L. Meridianens
Circul, igiennem huilcken Solen hafver sit Lob; Naar nu Solen er udi Zenith
M. da findis der ingen Parallaxis eller Wlighed aff deris Siun /
baade den som staar paa Jorden / oc den som staar (om mueligt var) udi
Jordens Centro eller Middelpunckt / fordi de seer da begge lige
op offver deris Hoffvet. Men dersom Solen var i D. da kunde den
Nederligere sees aff den som stod offven paa Jorden i B. end aff den som
stod i Jordens Centro C. Oc den Forskiel oc Wlijhed aff deris
Siun / som actis udi den Angulo eller Vinkel B.D.C kaldis Solens Parallaxis.
Jo nærmeere Solen kommer til Horizonten / jo meere Forskiel er
der paa / oc jo større bifver hendis Parallaxis.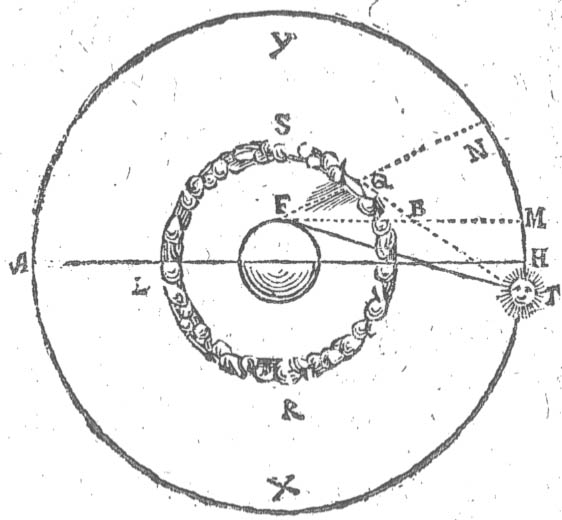

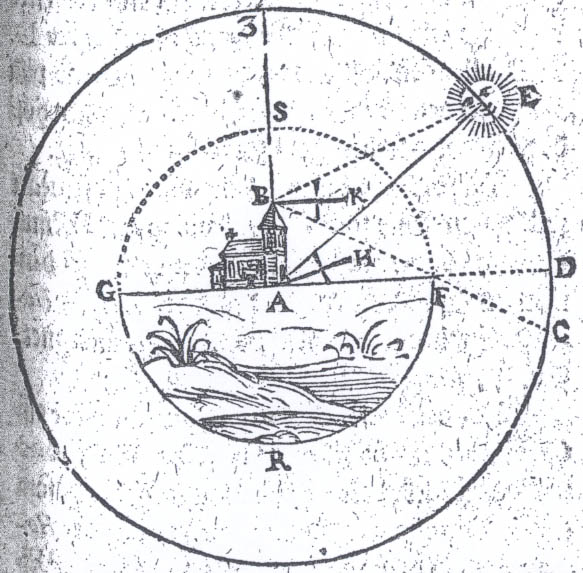
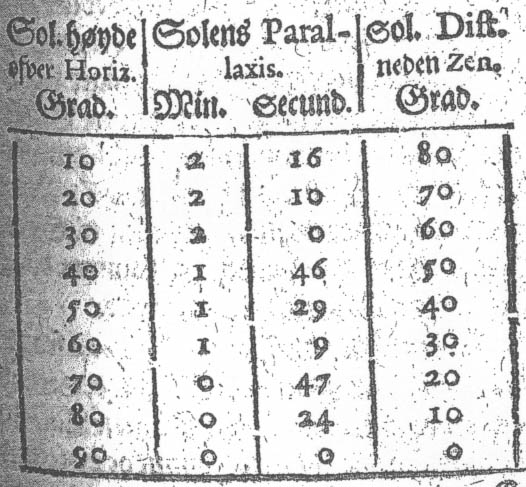 denne
Forskiel neden Zenith, (dog med Stiernerne actis det icke stort /
for den vijde Distantz som er mellem Jordens Centro oc
dennem:)[.] Thi naar den sees øverst på Jorden/ da sees den
nederligere/ end dersom mand saae den udaf Jordens Centro.
Huilcket nocksom tilforne udi denne Bog er demonstrêret udi
forklaringen paa de Matematiske Ord/ som udi denne Konst
brugelige ere / huis Figur findis der solvêret hos Forklaringen
paa det Ord Parallaxis, huor jeg vil hafve den fromme Læser
henviist. Oc efterdi voris Tafler om Solens Declination blifve
beregnede / lige som mand saae Solen aff Jordens Centro, da bør
mand ocsaa at observere den Forskiel / som der udi er at acte /
oc den retteligen forrekomme...
denne
Forskiel neden Zenith, (dog med Stiernerne actis det icke stort /
for den vijde Distantz som er mellem Jordens Centro oc
dennem:)[.] Thi naar den sees øverst på Jorden/ da sees den
nederligere/ end dersom mand saae den udaf Jordens Centro.
Huilcket nocksom tilforne udi denne Bog er demonstrêret udi
forklaringen paa de Matematiske Ord/ som udi denne Konst
brugelige ere / huis Figur findis der solvêret hos Forklaringen
paa det Ord Parallaxis, huor jeg vil hafve den fromme Læser
henviist. Oc efterdi voris Tafler om Solens Declination blifve
beregnede / lige som mand saae Solen aff Jordens Centro, da bør
mand ocsaa at observere den Forskiel / som der udi er at acte /
oc den retteligen forrekomme... Exempel.
Exempel. I
denne Figur lad B.R.Z.E.A.C.D. betegne Meridianen. R. Nord-Polen
/ oc C. Sønder-Polen. D.E. Æqvinoctialen. Z. Zenith, oc
M.N.O.P.Q. Jorden. B.A. Horizonten.
I
denne Figur lad B.R.Z.E.A.C.D. betegne Meridianen. R. Nord-Polen
/ oc C. Sønder-Polen. D.E. Æqvinoctialen. Z. Zenith, oc
M.N.O.P.Q. Jorden. B.A. Horizonten.




 offver
Horizonten. Samme 50 Grader subtrahêrer jeg atter igien
fra 90 Grader D.P.; da offverbliffver igien for A.P. 40 Grader / oc saa
meget er Nord-Polen under Horizonten. Huilcken Distantz er
lige med Syd-Polens Høyde i Sønden B.C. som jeg søgte.
offver
Horizonten. Samme 50 Grader subtrahêrer jeg atter igien
fra 90 Grader D.P.; da offverbliffver igien for A.P. 40 Grader / oc saa
meget er Nord-Polen under Horizonten. Huilcken Distantz er
lige med Syd-Polens Høyde i Sønden B.C. som jeg søgte. I
denne Figur er D.E. Æqvinoctialen. A.S. Solens Høyde i Norden
39 Grader / oc S.D. Nordlig Declination 14 Grad.
I
denne Figur er D.E. Æqvinoctialen. A.S. Solens Høyde i Norden
39 Grader / oc S.D. Nordlig Declination 14 Grad.
 I
denne Figur tager jeg Solens Distantz Z.S. fra Zenith mod
Norden 32 Grader / oc den Sydlig Declination D.S. 8 Grad.
I
denne Figur tager jeg Solens Distantz Z.S. fra Zenith mod
Norden 32 Grader / oc den Sydlig Declination D.S. 8 Grad. I
denne Figur er A.B. Horizonten, D.E. Æqvinoctialen / C.
Syd-Pol / oc F. Nord-Pol / Z. Zenith.
I
denne Figur er A.B. Horizonten, D.E. Æqvinoctialen / C.
Syd-Pol / oc F. Nord-Pol / Z. Zenith.
 I
denne Figur er P. nord-Pol / oc C. syd-Pol / E.D. Æqvinoctialen
/ S. Solen / Oc B.S. Solens Høyde offver Horizonten.
I
denne Figur er P. nord-Pol / oc C. syd-Pol / E.D. Æqvinoctialen
/ S. Solen / Oc B.S. Solens Høyde offver Horizonten.
