Oversat af Ivan Tafteberg Jakobsen

Oversættelse i uddrag fra
Petrus Apianus: Instrument Buch durch Petrum Apianum erst von new beschriben.
Ingolstadii, 1533. [Findes på Statsbiblioteket i Århus].

 

Den ottende og sidste del af denne

bog / om målestaven / hvis lige tid-

ligere aldrig er set. Derigennem vil flere og andre fremgangsmåder

 og nyttigheder / (som følger) også indtil nu af mange / som

 roser sig af at have forstand på de matematiske kunster /

 holdt for umulige / blive fremvist.

 

Det første kapitel / hvorledes målestaven

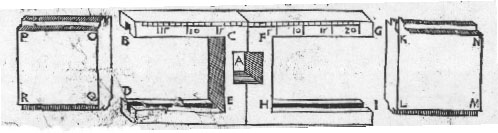
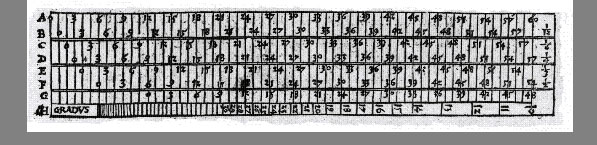
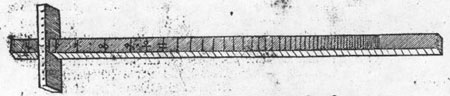
skal laves og tilvirkes.

Tag dig en lige / og firesidet lille stav / som er ren og velhøvlet / den ene side lige så bred som den anden. Og jo længere den lille stav er / jo bedre er den at benytte: ligesom jeg tidligere også har tilrådet det med andre instrumenter. Del denne stav i længden / i nogle dele / så mange som du vil / smalt eller bredt / som det passer dig : men efter mening er det bedre / når inddelingen er smal. Først (som jeg i det følgende vil vise dig ved en figur) betegn den ene og første side af staven med bogstaverne A / B / Den anden side lige ved siden af / med C / D. Den tredje med E / F. Den fjerde med G / H. Når du har opdelt en side i længden / det vil sige i lige store dele / de være sig mange eller få / så træk den samme opdeling hele vejen rundt på alle fire sider / som du herefter ser på figuren / hvor siden A / B / er opdelt i 60 lige store dele / og den samme del er trukket hele vejen rundt på alle fire sider : kun ved H’et står skrevet GRADUS. Dernæst følger en ulige opdeling / den skal ikke forstås her / men denne figur har jeg førhen brugt i en latinsk bog på denne måde. Imidlertid skal opdelingen på én side være ligesom på den anden. Det er ligegyldigt / om du deler staven på langs i 100 eller 1000 dele / det kan gå lige op eller ulige / det er lige meget. Fordi den ende af staven / der hvor bogstaverne A / B / C / D etc. står / hver gang skal sættes eller slås ved øjet / må du også påbegynde tallene for opdelingen ved A’et. Du kan også indskrive dig tal som du vil / over 2 / over 3 / over 4 / eller 5 / som du nu synes. Men jeg har i det følgende eksempel indskrevet det over 3 / så at der hver gang er et ciffer over 3 punkter / som du ser for dine øjne. Fordi sædvanligvis / (som du vil få at høre om lidt) er løberen 12 punkter lang: for 12 er det allerbedste tal / som lader sig opdele i mange dele / såsom i 12 dele / i 6 dele / i 4 dele / i 3 dele / i halve. Derfor sæt og ryk cifferet ved B’et / et punkt frem / det betyder 1/12 / Ved C’et ryk et punkt frem / og giv cifferet over for A’et 1/6 / Ved D’et 1/4 / ved E’et 1/3. Til sidst ved F’et skal du rykke 2 dele frem ( det vil sige med tallet eller cifferet) så giver den samme inddeling dig 1/2. På siderne G H / skal du straks rykke 12 punkter frem med cifrene : H’et skal ikke gælde noget på denne stav / men opdelingen af G skal alene sammen med cifrene helt optage siderne G / H . Altså er staven færdig på langs / som du ser det på denne figur.

 

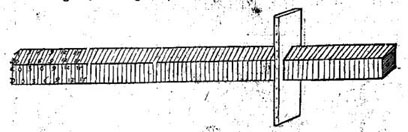
Det andet kapitel / om løberen

hvor lang den skal være.

 Når du har lavet staven på langs / så lav derpå et lille tværtræ / eller lille bræt / altså / lav et hul gennem midten / så at staven derigennem eller deri kan gå frem og tilbage vinkelret. Det samme lille stykke træ skal være nogle punkter langt / hvori stavens længde er opdelt / det være sig 12 / 60 / 100 etc. / hvilket tal du synes / men på denne figur har jeg lavet den 12 lang. Og det samme lille stykke træ eller lille bræt / vil i det følgende blive kaldt løberen. Så er staven helt og fuldstændig færdig til brug. Og den har denne form / som er aftegnet nedenfor.

 

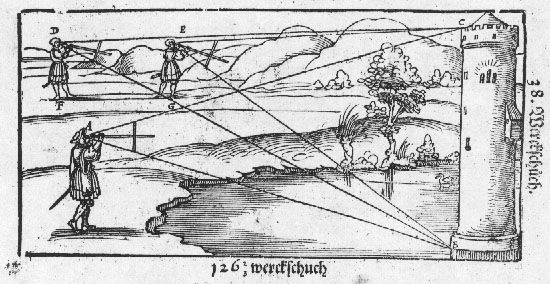
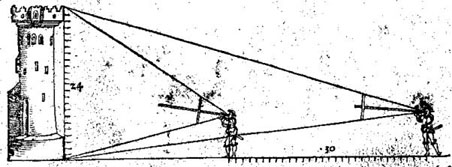
Det tredje kap. hvorledes du skal måle

højden af et tårn med denne stav / når du

står langt derfra / og ikke kan gå hen til det.

Et tårn skal du måle ved at tage sigte to gange således / Træd ind på en flad mark / hvor du kan gå frem eller tilbage / sæt så staven med bogstaverne til det ene øje / hold det andet lukket i / og vend løberen med den ene ende ovenover / og med den anden underneden / og ryk løberen frem og tilbage / indtil du kan se tårnets fod og spids ved siden af de to ender på løberen / og lav et mærke på jorden / lige ved din fod, og bemærk hvilket ciffer eller punkt indersiden af løberen berører ved bogstavet A. Jeg sætter at den berører punkt 21 i A : derfor opsøg 21 på inddelingen G / og anbring løberen her : gå så tilbage / på en ret linje / så langt / at du igen bringer spids og fod i synslinjen ved løberen : hvor du da står skal du igen lave et mærke ved din fod. Mål derefter fra det ene fodmærke til det andet / lige så mange alen eller skridt det er / lige så højt er det selvsamme tårn.

Ofte sker det / at du ikke kan gå tilbage / men frem / så må du i den første sigtetagning lægge mærke til hvilket på på opdelingen G løberen falder på. Jeg sætter / at den er faldet på punkt 27 / på G’et. Opsøg nu også punkt 27 på A’et / anbring løberen der / og gå mod tårnet / så langt at du bringer spidsen og foden af tårnet in sigte / og lav igen et mærke. Mål hvor mange alen eller skridt der er derimellem / de angiver dig hvor højt det selvsamme tårn er.

Til tider sker det / og det er ofte / at du ikke kan gå så langt tilbage eller frem som tårnet er højt : derfor lærer jeg dig at opskrive tallet / på en halv højde / og en tredjedel af højden / en fjerdedel / en sjettedel / og en tolvtedel. Da løberen er 12 punkt lang / så er et punkt deraf 1/12. Derfor er cifrene ved B’et / sprunget én over fra begyndelsen. Og bliver altså brugt når du  første gang har taget sigte på tårnet / og placeret mærket på jorden / og du kan ikke gå langt tilbage. Jeg sætter at løberen er ved punkt 9 på A / og du kan gå tilbage : ryk derfor løberen 

til 9 på B’et / og søg igen et ståsted bag dig / hvor du som før har sigte mod spids og fod / så vil så langt fra det ene fodmærke / som det andet står give dig tolvtedelen af tårnets højde.  Hvis du vil gå fremad / fra  første mærke og sigtetagning henimod tårnet / så tag punktet på C’et ved første sigtetagning / og anbring løberen ved dets tal ved A : så finder du også ved afstanden mellem de to standpunkter en 1/12 af tårnets højde.

I tilfælde af at du vil have en sjettedel af tårnet så brug tallet for punktet på A / på C’et / og omvendt søg først punktet på C / og dernæst på A / så angiver afstanden mellem standpunkterne 1/6 af tårnets højde. Jeg sætter at de to standpunkter er 16 skridt fra hinanden / og at det er en sjettedel / idet du har brugt C’et over for A’et : Tag nu 16 skridt seks gange / så har du tårnets højde / til 96 skridt.

Vil du have en fjerdedel af tårnet på jorden / så brug cifferet D. Vil du have en tredjedel / så brug E. F’et giver med sit tal tårnets halve højde. Således kan du på denne måde måle fra en sal / ud gennem et vindue / hvor højt et tårn eller en anden bygning kan være / især når punkterne ligger tæt og er små / og løberen er 20 / 30 / 60 / eller 100 punkter lang. For disse tal kan tåle særdeles mange opdelinger / som / 1/10 / 1/5 / 1/4 / 1/6 / 1/50 / 1/100 etc.  eftersom tallet er.

 

Det fjerde kap. hvorledes du alene ud fra

opdelingen af løberen og ud fra to sigte-

tagninger / som sker uden omhu (?) / skal

måle højden.

Endnu lettere kan du indrette dig en målestav / når du kun har et dårligt stykke træ uden nogen inddeling / in summa som ikke har nogen inddeling og heller ikke noget ciffer / kun løberen inddeles i 12 lige store dele. Tag et eksempel. Jeg sætter at løberen er inddelt i 12 lige store dele / og du står to gange / hvor det passer dig / stille / og afmærker med kridt eller knivspids / hvor løberen begge gange er anbragt / så træk løberen af staven / læg den op ad den ene kridtstreg / og bemærk hvor mange punkter på løberen der indbefattes  mellem de to sigtetagninger : hvis ellers  løberen så lang / at den når begge kridtstreger / hvis ikke / så skub den frem / så langt at du ved hvor mange punkter der indbefattes derimellem.

Jeg sætter at løberen (som før) er 12 punkter / og mellem de to kridtstreger er der 15 punkter / og mellem de to mærker på jorden er der 30 skridt. Sæt nu i reglen / punktet eller længden af løberen i midten / 15 frem / til sidst de 30 skridt / og og gør så efter regel detri / sig / 15 giver 12 / hvad giver 30? Det giver i følge reglen 24 skridt. Få forståelse ved hjælp af denne figur.

 

Det er ligesådan / når du deler staven / i så mange dele som du vil / jo tættere jo bedre : og gør løberen 100 punkter lang : men på løberen må der ingen inddeling være / fordi staven er inddelt. Når du måler dermed / så sæt hver gang to 00 nuller til skridtene / for de to sigtetagninger : dette samme tal skal du dele eller dividere op i stavens punkter / som er mellem de to kridtstreger. Du kan også lave løberen 1000 punkter lang (så du får brug for en rigtig lille inddeling) : så må du sætte 000 nuller efter skridtene / og derefter først dele. .../ Lad løberen være 100 punkter lang / mellem de to standpunkter på jorden 54 skridt eller alen / og 30 punkter mellem kridtstregerne : efter reglen kommer højden af tårnet til 180 skridt eller alen. Dennne stav vil jeg i det efterfølgende kalde den dårlige stav.

 

Det femte kap. hvorledes du skal måle højden af

 et tårn / med ét ståsted ved hjælp af den dårlige stav.

 Undertiden står et tårn på en plan flade / så at man kan gå til og fra det : det samme tårn kan opmåles særdeles let / således / træd hen til tårnet / og mål derfra enten i skridt eller alen / så langt og så meget du vil. Jeg sætter at du går120 favne derfra / målt med flid / og står stille : og når har taget sigte på tårnets fod og spids / så finder fra øjet til løberen 60 punkter / og løberen er 12 punkter lang. Sæt ind i reglen / 60 giver 12 som giver 120 favne. Få  ifølge regel detri 24 favne / så højt er tårnet. Mærk med flid / at de punkter der angiver / hvor lang løberen er / hver gang skal sættes i midten af regel detri. Det ovenfornævnte eksempel er øjensynlig indbefattet i denne figur.

 

 

Det sjette kap. hvorledes du skal måle

højden af et tårn / ved hjælp af den dårlige stav /

 hvor du står på jorden ved tårnet.

Når du står på jorden ved et tårn / og vil måle hvor højt det er / så se først efter / om det forneden og foroven har den samme bredde: er det smallere foroven / så tag også en sådan bredde forneden : det får du snart fat i ved hjælp af et blystykke (???). Når du har tårnets bredde / så mål hvor mange alen eller andet mål det er bredt. Jeg sætter det er 20 skridt bredt. Træd derpå hen for midten af tårnet / eller nogle skridt derfra / og ryk løberen frem og tilbage / så langt / til du bringer de to endepunkter på den samme side af tårnet til at være på en ret sigtelinje. og bemærk hvor langt løberen står fra dit øje.  Jeg sætter at det står 60 punkter derfra / og løberen er 12 punkter / Sæt ind i reglen / sig 12 giver 60 / hvad giver 20 skridt? ifølge reglen er tårnet 100 skridt højt / dertil lægger du din længde op til øjet / så har du den rette højde af tårnet. Ved denne måling og regel må du sætte de punkter der angiver længden af løberen på den første plads.

Eksemplet kan du tydeligt aflæse af denne hosstående figur.  

Det syvende kap. hvorledes du ved hjælp af

den dårlige stav skal måle / hvor langt der er

 til et tårn / og du kan ikke komme til tårnet

på grund af grave og andre hindringer.

 

Jeg siger om den dårlige stav / at fra den kan altid benytte inddelingen ved A’et / eller inddele en stav kun på én side / i lige store inddelinger / og gøre løberen nogle af de samme punkter lang. Hvis du således vil kende afstanden til tårnet / så mål først ved hjælp af to ståsteder (sådan som jeg har lært dig i det tredje kapitel) tårnets højde. Som det er vist på denne efterstillede figur ved de to bogstaver F og G / hvilket angiver det halve tårn. Tag denne længde to gange / så har du højden af tårnet på denne figur. Når du nu har højden af tårnet. Jeg sætter at den er 38 werckschuch høj / Nu vil du vide hvor langt der er fra bogstavet A til tårnet / så tag sigte på tårnet som du ved. Jeg sætter at løberen ved sigtetagningen bliver fundet at være 40 punkter fra øjet. Sæt ind i reglen / sig / 12 (det er løberens længde) giver 40 punkter fra øjet / hvad giver 38 werckschuch? Ved hjælp af reglen kommer der 126 2/3 werckschuch. Så langt er ståstedet ved A fra tårnet. Du kan få en bedre forståelse ved hjælp af den eftersatte figur. Det gælder ligegyldigt hvordan du finder højden af tårnet (?). Således / og på en sådan måde kan måle ud gennem et vindue / hvor langt du har over et stykke vand til et tårn / for hvilket du i forvejen har fundet højden.

 

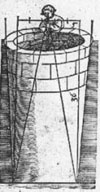
Det niende kapitel. hvorledes du ved hjælp af

staven skal måle dybden af en brønd.

Som du nu har for øje / at brønden sædvanligvis er bredere foroven end forneden ved vandet : derfor skal du først med et blystykke skønne / brøndens bredde ved vandet. Jeg sætter at brønden nede ved vandet er 5 schuch bred. Nu vil du kende dybden / så tag sigte på brønden til begge sider med staven / ligesom du har det for øje på figuren : og bemærk hvor mange punkter løberen står fra øjet / jeg sætter at den står 86 2/5 punkter fra øjet / Nu fastsætter reglen således / sig / 12 (det er løberens længde) giver 86 2/5 punkter / hvad giver 5 werckschuch? Gør det efter reglen / så finder du at brønden er 36 werckschuch dyb. 

Forståelsen af dette ovenforstående kan du få fra denne hosstående figur.

Det tiende og sidste kap. hvorledes du skal

 lave en almindelig løber / som du kan gøre stor

 eller lille / som nødvendigheden byder det.

Til tider / når du vil opmåle et vindue eller andet i det fjerne / så er løberen sædvanligvis for lang : derfor vil jeg lære dig at lave en almindelig løber / som du kan gøre lang eller kort. Lav en løber / som du ser på den eftersatte figur : og gør det sådan at du til begge sider kan skubbe et lille bræt derind / som lader sig føre frem og tilbage. Firkanten O / P / Q / R / skal gå frem og tilbage med siden O / P / i løberens B / C  : og ved O’et skal der være en viser (?) : og med linjen Q / R skal den gå frem og tilbage i D / E. Også firkanten K / L / M / N / på den anden side skal føres ud og ind : K / N i F / G og L / M i H / I : og ved K’et skal der også være en viser ligesom ved O’et. Lad dernæst en linje gå gennem løberens midte / som gennem A / og sæt på begge sider ud fra den samme linje / nogle punkter fra staven / og delt et sådant punkt igen i halve / dertil skriv cifferet for 5 i 5 / eller som det passer dig : nu gælder de halve punkter som hele punkter.

 

Når du vil bruge denne løber / så ryk de to firkantede småtavler hen på hvilket punkt du vil / som når du rykker viseren K hen på 5 punkter / på linjen F G / og ryk så viseren ved O’et hen på 5 punkter på linjen B / C / og brug linjen K L / og linjen O Q / som den rette løber : og i dette eksempel er det som om / du havde delt løberen i 5 dele / eller at løberen var så lang som 5 punkter på staven.

Her slutter denne bog.