Højdekurver (niveaukurver).

Download i Wordformat.

Download i pdf-format.

Hjælpemidler:

Håndniveau, vinkelprisme, målebånd, landmålerstokke.
(Nivellerinstrument kan anvendes i stedet for håndniveau).

Tekster:

Beskrivelse af nivellerinstrument.

Beskrivelse af håndniveau.

Beskrivelse af vinkelprisme.

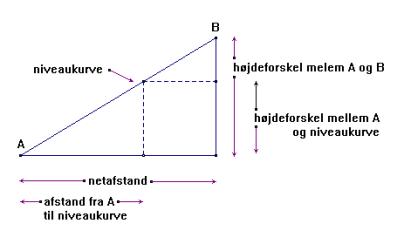
Formålet med øvelsen er at tegne et kort med højdekurver over et valgt område. En højdekurve (niveaukurve) er en kurve afsat på kortet således at alle punkter på kurven har samme højde (kote) i forhold til et givet udgangspunkt.

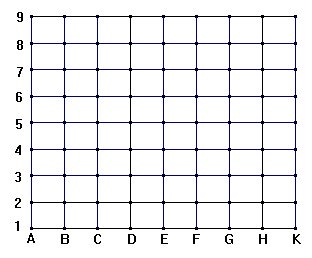
1.   Vælg et passende kuperet område på ca. 200 x 200 meter.
      Der skal være udsyn over hele området.

2.      Et kvadratnet udstikkes med vinkelprisme, målebånd og stokke. Der skal være ca. 25 meter mellem hvert punkt. Afstanden (den vandrette afstand) mellem alle punkter skal være den samme.

For at holde styr på punkterne benævnes de A1, A2, A3, osv.  

Diagonalerne i kvadratnettet kan bruges til at kontrollere nettet.

3.      Vælg det  laveste punkt P i  kvadratnettet som udgangspunktet. Bestem højdeforskellen fra P til alle punkter i kvadratnettet.
Hvis ikke alle punkter i kvadratnettet kan ses fra udgangspunktet P eller hvis højdeforskellen bliver for stor, vælges et punkt i kvadratnettet hvis højdeforskel fra P allerede er målt. Med dette punkt som nyt udgangspunkt bestemmes højdeforskellen til resten af punkterne i kvadratnettet.
Ved bestemmelse af højdeforskelle kan anvendes enten håndniveau eller nivellerinstrument.
Lav et skema hvor alle målinger omhyggeligt indskrives. Skemaet kan ses sådan ud:

 
      Stokkene i nettet må ikke tages ned før alle koter er beregnet.

4.      Højdeforskellen mellem højdekurverne kan vælges til fx at være 1 meter.
Højdekurvernes skæring med siderne i kvadratnettet findes ved lineær interpolation
Lav et overskueligt skema, hvor alle de fundne skæringspunkter indsættes.

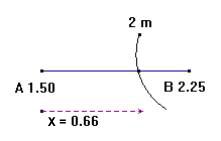
Eksempel på interpolation:
Her er vist hvordan man bestemmer, hvor højdekurven der svarer til 2 meter skærer kvadratnettet mellem to punkter A og B hvis niveau er målt til hhv. 1,50 m og 2,25 m.

På figuren er afstanden mellem A og B 1 meter (netafstanden), og x er afstanden fra punktet A til højdekurven:  

x  =   = 0,66.

     I udregningen er brugt at afstanden mellem A og B er 1 m (netafstanden).
     Hvis den ikke er 1 m skal x ganges med afstanden mellem A og B.

Formel, der ovenfor er brugt til interpolation kan generelt skrives som:  

Lodret snit af terrænet mellem A og B.

5.      Højdekurverne tegnes ind på et millimeterpapir.
Tegn først kvadratnettet ind.
Afsæt dernæst niveaukurvernes skæringspunkt med kvadratnettet.
Højdekurverne tegnes blødt gennem skæringspunkterne.

6.   Højdekurverne kan også tegnes ved at indtaste de målte højdeforskelle i et Mathcad-program.

      Hent Mathcad programmet HØJDEKURVER.  Programmet kan kun åbnes i Mathcad og forudsætter at kvadratnettet består af 6 gange 6 stokke.